Thermodynamics Crib Sheet
Index
1 Introduction.2 Zeroth Law.
3 First Law.
3.1 Ideal Gas Law.
4 Second Law.
4.1 Heat Engines.
5 Entropy.
5.1 Irreversible Processes.
5.2 Isothermal Process.
5.3 Adiabatic Process.
5.4 Carnot Engine.
5.5 Engine Efficiency.
5.6 Entropy.
5.7 Restatement of Second Law.
6 Enthalpy.
7 Gibbs Free Energy.
8 Third Law.
9 Kinetic Theory.
9.1 Energy Distribution.
9.2 Maxwell-Boltzmann.
9.2.1 Velocity Distribution.
9.3 Bose-Einstein Distribution.
10 Black Holes.
11 References.
1 Introduction
Basic Concepts
Thermodynamic systems are described by a number of physical variables such as volume and pressure, spin, electromagnetic field strength and direction, etc. All the possible states the system can be in form a state space, a subset of RN. Systems in thermodymanic equilibrium are (i) in physical contact, (ii) "heat" can flow freely between them and (iii) the state of the system does not change over time (hence "equilibrium").
The requirement for physical contact could probably be relaxed, but the more limited definition works fine for the purpose of defining temperature. (See below)
What is temperature? It is not obvious that temperature is a well-formed concept. Other concets, such as pressure, are intuitive but turn out to be more subtle than expected. For example, the forces in a moving fluid are often better described by a stress tensor than a single "pressure" scalar.
2 Zeroth Law
If two systems are in thermal equilibrium with a third system, then they are in equilibrium with each other.
The Zeroth Law allows temperatures to be consistently assigned to equilibrium states. Systems in thermal equilibrium are said to be "at the same temperature".
Lemma: The relation © = "is in equlibrium with" between thermodynamic systems is a equivalence relation.
Proof: Need to show that the relation is (i) transitive, (ii) symmetric and (iii) reflexive.
The Zeroth Law is a statement that the relation is transitive. I.e. if A © B and
B © C then
A © C.
The relation "is in equilibrium with" is symmetric by definition.
It is trivial to extend the relation so that A © A. QED.
A temperature function can be defined by assigning the same temperature to each state in the equivalence class. The temperature so defined may indeed not look like the Celsius temperature scale, or even be continuous, but it is a temperature function. In some systems, states of constant temperature may form smooth surfaces in the state space in which case the normal provides a natural ordering of nearby surfaces. It is then simple to construct a global temperature function that provides an continuous ordering of states. For example, if two systems of ideal gas are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the 'amount' of gas. The surface PV / N = const defines surfaces of equal temperature, and the obvious (but not only) way to label them is to define T so that PV / N = RT where R is some constant. Such a system can be now be used as a thermometer to calibrate other systems
Is temperature defined for non-equlibrium systems? For example, how does the definition of temperature defined from the Zeroth Law extend to turbulent fluid flow? The answer is to (i) apply equilibrium thermodynamics to "finite elements", and/or (ii) associate temperature with energy. (See below)
Definition: An Isothermal is a surface of constant temperature in the state space.
3 First Law
Energy is conserved. Heat is a form of energy.
For any system, DU = Q - W where U = internal energy, Q = heat added to the system, W = work done by the system.
3.1 Ideal Gas
The relationship PV = NRT can be established experimentally.
(There is some circularity here since the equation is partial motivation for the choice of temperature function)
Consider cube of side L filled with N molecules of an ideal gas. Assume the molecule moves from one wall, to the opposite wall and back.
Average impulse on wall per molecule
= <F>
For N molecules,
Þ P = <F>
Þ P = (Nm
Þ P = Nm
Þ PV = ⅓ Nm <v2>
Þ PV = NRT
Þ NRT = ⅓ Nm <v2>
Þ T = m
Þ T = ½ m<v2> 2/3R
Þ T= ⅔
|
PV = 2/3 N <E> = NRT |
4 Second Law
4.1 Heat Engines
A heat engine is a device that absorbs an amount of heat Qh from a hot reservoir, exhausts an amount of heat Qc to a cold reservoir and does work W.
Kelvin-Plank Statement of the Second Law: It is impossible to extract an amount of heat Qh from a hot reservoir and use it all to do work W. Some amount of heat Qc > 0 must be exhausted to a cold reservoir.
The second law states that it is impossible to build a perpetual motion machine. Any real-world motion generates heat through friction, and the 2nd law states that not all of the generated heat can be turned back into work.
5. Entropy
5.1 Irreversible Processes
An irreversible process goes only in one direction. I.e. the system and the universe cannot be put back into the initial state. Assertion: A process is reversible if and only if it only passes through equilibrium states that are “quasi”-static. Any non-equilibrium state renders the process irreversible. The proof? Good question.
There is no such thing as a “quasi-static” state. It is a useful construct. There is no such thing as a truly reversible process in nature.
In general dQ = dU + dW is not an exact differential. I.e. ![]() so the heat absorbed / released depends on path taken between states.
so the heat absorbed / released depends on path taken between states.
5.2 Isothermal Process
The temperature remains constant in an Isothermal process. For an ideal gas, ![]()
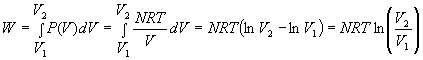
5.3 Adiabatic Process
No heat is absorbed during an Adiabatic process. For an ideal gas, ![]() .
.
dQ = 0 for Adiabatic processes, so dU = -dW
Þ ![]()
Þ ![]()
Þ 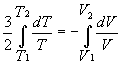
Þ ![]()
Þ 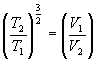
Þ Put g = 5/3, then T1V1 g-1 = T2V2 g-2. Substituting T = PV/NR gives P1V1g = P2V2g.
Þ 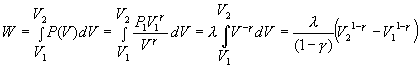 where l = P1V1g
where l = P1V1g
5.4 Carnot Engine
The most efficient heat engine possible. (If a more efficient engine could be built, the more efficient engine could be used to drive the Carnot Engine as a refrigerator and produce perpetual motion) The engine cycle consists of 4 stages shown in the P-V diagram below.
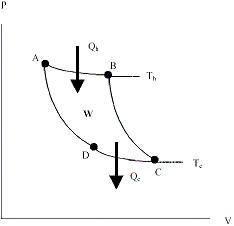
The four stages are
- Isothermal expansion at temperature Th . A quantity of heat Qh is absorbed from the heat reservoir. (state A® state B). DU=0, WAB = NRTh ln(VB/VA)
- Adiabatic expansion (state B® state C). DU=3/2NR(Tc-Th.), WBC = -DU
- Isothermal compression at temperature Tc. A quantity of heat Qc is absorbed from the heat reservoir. (state C® state D). DU=0, WCD = NRTc ln(VC/VD)
- Adiabatic compression (state D ® state A). DU=3/2NR(Th-Tc.), WDA = -DU
Total work done in 1 cycle = WAB+ WBC+ WCD+ WDA = WIsothermal + WAdiabatic
WIsothermal = , WAdiabatic = -DUTotal = 0 since the cycle is a closed path which saves doing a great deal of algebra.
5.5 Engine Efficiency
Efficiency E is defined to be ![]() . For a Carnot Engine,
. For a Carnot Engine,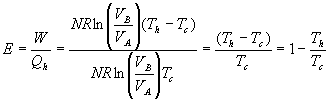 .
.
5.6 Entropy
The following relationship holds for a Carnot engine: Qh /Th =
Qc/Tc Þ 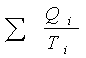 = 0.
= 0.
The area inside any closed path can be approximated by Carnot “tiles” as shown in the diagram below. . I.e. there exists a function S, called Entropy, that for any path from A to B.

The relationship between entropy, heat and temperature is often stated in the simplified form as DS = Q/T where S = entropy, Q = heat flow, T = temperature.
The second law implies that for a non-Carnot engine 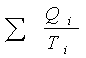 ³
0. I.e. DS ³
0.
³
0. I.e. DS ³
0.
Query: If any cycle can be approximated by a mesh of Carnot engines, and DS = 0 for Carnot engines, then why doesn’t DS = 0 for all engines? Answer: The Carnot engine assumes an Ideal gas operating in a perfect environment. Real-world engines are more wasteful with their heat flows so DS ³ 0.
5.7 Restatement of Second Law
In any cyclic process the entropy will either increase or remain the same.
6 Enthalpy
For systems characterised by pressure and volumne, Enthalpy H = U + PV where U = internal energy, V = volume of system, P = pressure.
At constant pressure, dW = PdV, so dQ = dU + PdV = dH
7 Gibbs Free Energy
Gibbs Free Energy = G = H - T.S where H = enthalpy, T = temperature and S = entropy.
DSuniverse =
The sign of
D G < 0: the reaction is spontaneous.D G = 0: the reaction is at equilibrium.D G > 0: the reaction is not spontaneous.
8 Third Law
It is impossible to cool a body to absolute zero by any finite process. What is absolute zero?
Nernst’s Heat Theorem: If it is possible to reach absolute zero, all systems at that temperature would have the same entropy (defined to be zero). In particular, as T ® 0, S ® 0.
Corollary: A body at absolute zero is associated with a definite energy called the zero-point energy.
9 Kinetic Theory
9.1 Energy Distributions
f (E) = probability distribution for particles with given energy. Three versions:
- Maxwell-Boltzmann Distribution (Classical):
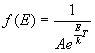
- Bose-Einstein Distribution (Indistinguishable bosons):
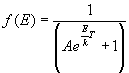
- Fermi-Dirac Distribution (Indistinguishable fermions):
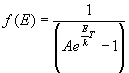
9.2 Maxwell-Boltzmann
9.2.1 Velocity Distribution
Let dN = F(vx ,vy ,vz) dvxdvydvz where F is the velocity distribution function, dN is the number of particles with velocities in the x,y,z direction in the intervals vx ® vx+dvx, vy ® vy+dvy, vz ® vz+dvz
Assume x,y,z are orthogonal and vx,vy,vz are independent, then F(vx ,vy ,vz) = f(vx)g(vy)h(vz)
Assume isotropy, then F(vx ,vy ,vz) = f(vx)f(vy)f(vz)
Isotropy implies also F(vx ,vy ,vz) = Y(v) for some Y where v = (vx2 + vy2 + vz2)½
Hence F = Y(v(vx ,vy ,vz)) = f(vx)f(vy)f(vz)
Differentiating:
Þ 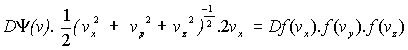
Þ 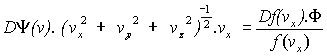
Þ 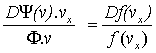
Þ 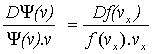
Þ .![]() ,
,
![]()
9.3 Bose-Einstein Distribution
Historically this was a VERY HARD problem - understanding black body radiation. Planck came up with a solution by assuming E = nhw where h = planks constant, w = frequency, and began the quantum revolution.
Black Holes[1]
Black holes are completely described by their mass, charge and angular momentum Þ T2 violated.
- 1970: Demetrious Christodoulou, Steven Hawking show area of event horizon of black hole always increases.
- 1970: Jacob Berkenstein suggests area of black hole can be used as measure of entropy. Generalised T2 (GT2) proposed.
- 1974: Hawking shows black hole emits black-body radiation ̃ Christodoulou-Hawking theorem fails under these conditions. Hawking radiation ̃ 1 bit of entropy per A/4 units of event horizon where A = planck area. Estimates of 1cm diameter black hole entropy = 1066 bits.
- 1980: Jacob Bekenstein proposes Universal Bound. Since any system is less dense than a black hole, and can be eaten by a black hole where it contributes at most A/4 to surface area, the total entropy of any system must less than A/4 where A is planck area of system boundary.
- 1986: Rafael Sorkin showed GT2 (or something very similar) must be valid for any conceivable black hole process (including emitting Hawking radiation).
- 1995: Leonard Susskind proposes Holographic Bound. A system is "induced" (???) to collapse to a black hole where it contributes at most A/4 to the surface area. The total entropy of any system must have been less than A/4 where A is planck area of system boundary.
Common sense suggest that the entropy of a system (e.g. computer chip) is related to volume (more chips = more entropy). Volume of system proportional system diameter3. Boundary (area) of system proportional system diameter2. Expect volume (and hence entropy) to outpace boundary area and so exceed holographic bound. Actually system collapse into black hole before bound can be exceeded!
- 1993: Gerard 't Hooft propose Holographic Principle. Boundary of system contains same information as system. Isomorphisms exist between system physics and physics defined on boundary.
- 1997: Juan Maldacena conjectured 4D flat universe maps to 5D anti-de Sitter universe. 5D Superstring physics maps to 4D Quantum field theory of point particles. 5D black hole maps to hot 4D radiation. Later confirmed.
- 1999: Raphael Busso proposed modified holographic bound that works even if boundary is not closed. (e.g. Open universe) Boundary determines entropy bound for region of space-time "illuminated" by a burst of light emitted perpendicular to surface. Light rays must initially be convergent, and excludes regions after light rays have crossed each other.
Many alternative bounds have been proposed. Universal bound more restrictive than Holographic bound.
Holographic bound restricts the number of degrees of freedom inside a surface, however QFT and Superstrings allow infinite degrees of freedom Þ QFT and Superstrings cannot be the final story.
Comments
Please feel free to send suggestions on how this page could be improved to the author Shaun O'kane. I will no longer respond to comments challenging the relationship between the Zeroth Law and temperature. Please note that articles on Wikipedia are sometimes spectacularly inaccurate.
References
[1] "Information in the Holographic Universe" by Jacob D. Bekenstein. Scientific American, August 2003.
Copyright © Shaun O’Kane, 2000, 2001, 2003