Quantum Reality
Why another page on Quantum Reality?
Many years ago when I was at university I alternated between the Mathematics and Physics departments for various subjects. The Physicists were an impressive lot, demonstrating mastery of Electromagnetism, planetary orbits, heat transfer and the like. Their mission was to come up with solutions and mathematics was a tool. Terms in equations were ruthlessly crossed out, substituted or ignored and the final results closely matched observed reality.
But then I would cross over to the Mathematics department where I would be assailed with pathological examples of functions and sets that defied common sense. In the end the mathematicians spooked me enough not to completely trust anything without examining it closely.
I decided to investigate Quantum Reality.
I am not a historian or philosopher, and this has influenced the work. For example, the Copenhagen Interpretation is presented with a "broad brush". Hopefully Bohr and Heisenberg would have recognised it, but few references are provided to backup any particular statement. With the passage of time it has become more and more difficult to get agreement on what a particular interpretation is, if that was ever possible in the first place. Bohr and Heisenberg didn't agree on everything, but, like the Bible, modern proponents seem to be able to find something in their writings to claim backing for just about any position.
It can be argued that that the views of Bohr and Heisenberg have become mainly of history interest; arguing over who-said-what hardly advances the Physics. The basics tenets of the Copenhagen remains intact but the details of the interpretation have evolved. For example, Bohr's Complementary Principle is now identified by many with frameworks in Consistent Histories.
This investigation began as a survey (almost everything in the first part of this document can easily be found elsewhere) but in the end, it was almost impossible not to be persuaded by one particular viewpoint. I also found it almost impossible to disguise my position, and sometimes I do not even try. I will leave it to the reader to discover why.
This document is divided into three parts:
- Part A looks with the various interpretations of Quantum Mechanics.
- Part B deals with the measurement process, which turns out to be a surprisingly rich topic.
- Part C presents the London (Ticker Tape) Interpretation of Quantum Mechanics - it is the result of the author's investigation in Part A and Part B. A separate overview can be found at
 |
http://www.bowmain.com/QM/London_Interpretation.pdf |  |
Note that the original London Interpretation document will no longer be updated (except to fix embarrassing mistakes). Further musings can be found at http://www.bowmain.com/QM/London_Interpretation_Part2.pdf. This document will be updated in the near future.
Philosophical terminology is kept to a minimum. HTML does not lend itself well to mathematical notation, so mathematics is kept to a minimum. The more technical arguments relating to this topic can be found in the pdf version of this document. See Index at the top of this page.
Please feel free to email me if you find an error anywhere in this article.
The most up-to-date version is prep work for an book. This version has had some proof-reading.
The pdf version of this document is more complete than this webpage which is quite old.
Contents
Part A - Interpretations
1. A Survey of Interpretations
- Copenhagen Interpretation
- State Vector Interpretation
- Consciousness Causes Collapse
- Many-world Interpretation
- Hidden Variable Theories
- Transactional Interpretation
- Extended Probability and Quantum Logic
- Consistent Histories
- Decoherence
2. Philosophy
- Francis Bacon
- Galileo
- Rene Descartes
- Immanuel Kant
- Positivism
- Niels Bohr
- Karl Popper
- Thomas Kuhn
- George Polya.
- Kant and Copenhagen.
3. Paradoxes, Phenomena and Proofs
- The Waveform that refuses to collapse
- Schrodinger's cat
- Wigner's Friend
- EPR
- Von Neuman's impossibility proof
- Bell's in-equality
- Closed system waveforms
- Consciousness
- Do Hidden Variable Theories have any value?
- Probability
- Feynman Sum of Histories
4. Conclusion
Part B - Measurement
5. Time
6. Measurement
- Principle of Real Measurement
- Principle of Exact Measurement
- Principle of State
- Principle of Repeatability
Part C - The London (Ticker Tape) Interpretation of Quantum Mechanics
- Mach Devices
- Principle of State
- Principle of Relativity (Mach's Principle)
- Equivalence Principle
- Derivation of Standard Quantum Mechanics
- The Calibration Problem
10. So what have I learnt about Quantum Mechanics?
of
Quantum Mechanics
1. Interpretations
There are as many interpretations of Quantum Mechanics as there are lawyers in the world (too many) so I have chosen only to investigate the more popular, or those I find particularly interesting.
1.1 Copenhagen Interpretation
This is the dominant view within the Physics community, and for good reason, however it is very difficult to actually find a definitive statement of exactly what the Copenhagen Interpretation is. In fact, there are multiple subtle versions of it. The main variant historically is presented below.
Synopsis: The Copenhagen Interpretation is a Positivist interpretation (See Below). The quantum world can only be examined by constructing machines that perform measurements. Quantum Mechanics is a probability calculus which can be applied to a specific combination of measuring devices and quantum system. The waveform is not "real"; it is a mathematical construction that represents the observer's knowledge of the system. No deeper level of understanding is possible.
What is a measuring device?
This is a really tough question. We shall go with the following definition,
although it is obviously incomplete and is revised later in the document:
A measuring device is a thing which produces a real valued outcome to an experiment.
i.e Measuring devices measure
"quantities" such as position, momentum, energy, charge etc whose values are
real numbers. Measurements never return complex numbers. To avoid confusion
with other uses of the word "real", we shall use ![]() to indicate the set of real numbers and the term
to indicate the set of real numbers and the term ![]() -valued
to indicate a quantity which takes a value which is a real number.
-valued
to indicate a quantity which takes a value which is a real number.
How can we tell what we are measuring? Bohr's view was that measuring devices are "essentially classical" in the sense that (1) they deal with classical concepts such as position, momentum etc. and (2) the examination of their macroscopic structure determines what they measure. There are problems with this view. (See below) Whatever it's shortcomings, this is the standard view repeated ad nauseum in text books. We shall have more to say on this topic later.
The following have historically been associated with the Copenhagen Interpretation.
Born's Probability Interpretation
What interpretation can be attached to wave function? The square of the amplitude of the waveform yields the probability density function. This is consistent with experiment (e.g. Diffraction experiments where single photons can be detected) and is not disputed by any of the interpretations (Hidden Variable Theories view the probability description as incomplete). The notion is generalized to the norm of the state vector in a Hilbert space.
Heisenberg's Uncertainty Principle (HUP)
The Copenhagen Interpretation objects to statements such as "It is not possible to measure the momentum of an electron without disturbing it's position". HUP makes no statement about "disturbing" anything, only that simultaneous measurements are not possible. In fact, as we shall see, the position of an electron may not even be well defined. HUP is a consequence of the mathematical structure of Quantum Mechanics and not directly challenged by any interpretation.
Observer Created Reality
Copenhagen does NOT say that the observer creates reality, whatever that means. It does not say that the world is a purely mental construct (Idealism).
Copenhagen does say that a property of a system however may not be defined until it is measured. For example, if an electrons waveform is smeared out over space, it's position is not just unknown but undefined. The electrons position is only defined once it is measured. Copenhagen treats the experiment and measuring apparatus as a gestalt (whole). The interested reader is referred to the later section on Philosophy.
Bohr's Complementary Principle or Wave-particle Duality
Quantum particles are said to exhibit a wave-particle duality. Bohr's Complementary Principle says that it is possible to design an experiment to show the particle nature of matter, or show the wave nature of matter, even though each picture of matter is mutually exclusive.
For example, Double Slit Diffraction using a single photon at a time demonstrates the wave-nature of light as the light moves from the source through the diffraction grating and builds up a diffraction pattern on the final screen. The particle nature of light is demonstrated by arrival of discrete packets of energy (photons) at the final screen.
Bohr’s Complementary Principle is at the heart of the Copenhagen Interpretation. Matter is neither a wave nor a particle; each picture is complementary not contradictory. It is the nature of the experiment which "chooses" which picture (or aspect) of matter is demonstrated.
The Principle is much more subtle and deep than it first appears; it is best understood by reference to Kantian or Positivist Philosophy. We know the world through our senses, or experimental devices. What we know about the world is as much a product of the devices we use to interact with the "real world" as the "real" world itself, which ultimately lies beyond our senses and essentially unknowable.
The author recommends that the reader re-visit this topic after reading the sections on Philosophy in the rest of this document.
Is the Waveform real?
The standard version of Copenhagen is clear on this issue. Consider the following statement by Bohr.
There is no quantum world. There is only an abstract physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.
The Copenhagen Interpretation regards the waveform as not real. The alternative interpretation which accepts the same probabilistic world-view as the Copenhagen Interpretation but regards the waveform as real will be referred to as the State Vector Interpretation.
Waveform Collapse
The Copenhagen Interpretation makes no comment on waveform collapse. The waveform is viewed as having no reality and is only an aid to calculating probabilities. Consider the following experiment:
A coin is to be thrown from the dark onto a table top. The observer cannot see the coin so the best description he can produce is
The coin tumbles onto the table and settles heads up. The best description of the coin is now
At no time did the description effect the outcome of the experiment and so in this sense it has no reality and the "collapse" of the waveform Y holds no mystery.
The coin example can also be misleading. We are quite happy to accept the "non-reality" of the waveform because we "know" the coin's position and momentum are in well defined states that could be measured, and if the appropriate calculations performed, we could determine in advance which way up the coin would land. The Copenhagen Interpretation on the other hand says the waveform is everything that is knowable about the experiment.
1.2 State Vector Interpretation
Synopsis: This interpretation is the interpretation usually implicitly presented in many physics text books. It accepts the Born Probability Interpretation and the belief that the ultimate description of the universe is probabilistic. The main difference from Copenhagen is that quantum systems are viewed as being in a state described by a wave function which lives longer than any specific experiment. The waveform is considered to be an element of reality. Measurement implies the collapse of the wave function. Once a measurement is made, the wave function is no longer smeared over many possible values, instead the range of possibilities collapses to the known value. Unfortunately the nature of the waveform collapse is problematic and the equations of Quantum Mechanics do not cover the collapse itself.
1.3 Consciousness Causes Collapse
Synopsis: It accepts most of the State Vector Interpretation except measuring
devices are also regarded as a quantum systems. This has some interesting
consequences:
If the measuring device is a quantum system, the measuring device changes state
when a measurement is made but it's wavefunction does not collapse. So when
does the waveform collapse? See The Measurement Problem below. The
collapse of the wave function can be traced back to its interaction with a
conscience observer. Seriously scary!!!
1.4 Many-worlds Interpretation
Synopsis: All possible outcomes are regarded as "really happening" and somehow we "select" only one of those realities (universes). Real SF stuff. Also untestable unless someone comes up with a way of moving between universes. First formulated by Everett.
If |a> and |b> are possible outcomes, then so is c|a> + d|b> for any c,d where |c|2 + |d|2 = 1 so the number of alternate universes is infinite. Since "every possible outcome" is viewed as happening, the many world interpretation implies universes where the laws of physics hold but every toss of a coin has resulted in "tails"! Universes "interfere" with each other "smearing" our universe at the quantum level. Making a measurement "selects" one of these universes.
Proponents of this theory suggest that the many-worlds interpretation of Quantum Mechanics is now the dominant view within the physics community. If true, this is undoubtly due to similarities between many-worlds and Feynman's approach (See below).
1.5 Hidden Variable Theories
Synopsis: Usually proponents have philosophically objections to what Einstein would call "God playing dice". It views electrons and other quantum objects as having properties with well-defined values that exist separately from any measuring device. (e.g. position and momentum) Quantum Mechanics is viewed as a high level statistical description of the underlying theory. Deterministic theories imply that the fate of universe was determined at creation and free will is an illusion. This view was favoured by Einstein and others.
The terminology "Hidden Variable Theories" is misleading. Many Quantum theories have "hidden" variables within their formulation. A better term would be "Deterministic theories". However we maintain what has now become a universally accepted convention and will also continue to call such theories Hidden Variable theories.
Hidden Variable Theories may or may not consider the waveform to be an element of reality. I.e. It may be purely a statistical creation, or it may have some phyiscal role (e.g. Bohm).
1.6 Transactional Interpretation
Synopsis: The statistical nature of the waveform is accepted but the waveform is broken up into an "offer" wave and "confirmation" wave, which both are "real". Quantum particles interact with their environment by sending out an "offer" wave. Probabilities are assigned to the likelihood of interaction of the offer wave with other particles. If a particle interacts with the offer wave, it "returns" a confirmation wave to the offer source. Once the "transaction" is complete, energy, momentum etc is transferred as a quantum as per standard Quantum Mechanics.
In the Transactional Interpretation, one would be expected waveform collapse to occur "at the first opportunity", thus resolving the waveform collapse problem. Is this tenable? Once collapse occurs, classical probability theory would apply rather than Quantum probability. This is not consistent with Feynman's Interpretation. e.g. How do virtual particles interact? To remain viable the Transactional Interpretation is forced to defer wave collapses to some unknown time and the forward, and retarded waves cease to have the required interpretation. The returning "confirmation" wave is typically smeared out over space (it is a wave!) so it unclear when the transaction begins, or when it is complete or how the confirmation wave determines which offer wave it matches up to.
1.7 Extended Probability and Quantum Logic
Synopsis: These attempt to reformulate Quantum Mechanics as probability or logic theories. The study of alternative theories of probability would be a valid and interesting area of research even in the unlikely event it was shown to have no relevance to Quantum Mechanics.
Extended probability: Are there alternatives to the standard Kolmogorov probability axioms? One of the more compelling derivations of probability axioms from desiderata is due to Cox. It appears that the alternatives to standard probability theory are limited, however the requirement for probability values to be real numbers can be relaxed. The resulting non-real probabilities correspond to quantum waveforms, however so far the approach has failed to produce truely compelling results (in the author's opinon).
Useful links: http://physics.bu.edu/~youssef/quantum/quantum_refs.html
1.8 Consistent Histories
Synopsis: Sometimes regarded as a variant of Copenhagen. Approach as per Bohr's Complementary Principle. The observer chooses a set of operators (corresponding to a choice of measuring devices) to analyse a specific situation. Each choice of operators, called a framework, establishes a set of outcomes that can be talked about (i.e. it establishes a sample space). It can be shown events in each sample space can be analysed using standard boolean logic and probability theory, provided that the set of outcomes are consistent. Events in separate sample spaces cannot generally be combined using standard logic. (Pure Bohr)
Some author's claim Consistent Histories is "Copenhagen done right", but Consistent Histories is often expanded to include a real waveform and decoherence as an essential part of the measurement process, which is inconsistent with Copenhagen. This document does not consider Consistent Histories as a stand-alone interpretation; instead we shall analyse the components of Consistent Histories separately.
1.8 Decoherence
Synopsis: The waveform is regarded as an element of reality. The measuring device is regarded as a Quantum system. When a measurement is made using “realistic” devices, the interactions of the combined system (target system and measuring device) with the external environment results in the waveform moving rapidly and continuously toward stable ‘pure’ (eigen)states.
Caveat: The term decoherence is somewhat ambiguous. It is commonly used in the Many-Worlds interpretation to indicate the selection of a universe (which corresponds to the separation of a superimposed state into the “pure” states associated with each universe). That is a discontinuous process.
Decoherence is at odds with the discontinuous behaviour observed in the photo-electric effect and other processes. (In the Photo-electric effect, a metal surface is bathed in radiation. The waveform describing emitted photons is evenly distributed across the entire metal surface, until a photon is emitted discontinuously)
Decoherence has become an increasingly popular concept in recent years, along with the related topic of Quantum Computing. However Decoherence is little more than a general engineering specification elevated to the status of an interpretation: a macroscopic measuring device must be engineered so that it (a) moves rapidly to a stable state once a measurement is made and (b) does so by interacting with the external environment and measured system. Not all Quantum systems behave that way. Decoherence, apart from being at inconsistent with observation, suffers from the same problems as all other real waveforms and will not be considered separately.
2. Philosophers
Disclaimer: The philosophy material below is greatly simplified and so may lack many of the subtleties of the original works. I am not a trained philosopher. If you find this area of interest or useful, you should conduct further study elsewhere. (E.g. via Google)
A understanding of the work of philosophers is necessary to understanding much of the published discussion on quantum interpretations. It is also useful in countering those who overstate positions. e.g. "Concepts which cannot be measured have no place in science" or "Science reveals the secrets of nature". It is also very interesting to discover just how much rubbish has been written over the years, and how long it took for an accurate view of what Science actually is to develop.
To appreciate the contribution of various philosophers it is necessary to understand the historical context. At the beginning of the renaissance, the pursuit of scientific knowledge was not distinct from the pursuit of theological knowledge. Since nature is the work of God, every scientific idea has theological consequences and was subject to the scrutiny of the Church. It is fair to say that the Church adopted positions based on highly subjective interpretations of scripture. One of the most famous examples of this was the rejection of the Copernicus' view that the sun was at the centre of the universe, and not the earth. The Bible was regarded as clearly stating that man was at the centre of the universe and so Copernicus simply had to be wrong. (E.g. Joshua 10:12-14. God stopped the sun in the heavens and extended the daylight hours for Joshua and his army to finish the battle with the Amorites) The views of the Church could not be taken lightly. It suppressed the idea until (and some time after) the invention of the telescope showed moons orbiting Jupiter. Clearly not everything revolved around the earth after all.
The following philosopher/scientists made notable contributions.
2.1 Francis Bacon (1561 - 1626)
Denounced the reliance on authority and argument divorced from the real world. He called for reasoning based on inductive generalization of observation and experiment.
2.2 Galileo (1564 - 1642)
Applied geometry to the laws of motion and created the science of mechanics. His success emphasized the usefulness of applying mathematics to the science. Not really a philosopher, more of a model of a practising scientist.
2.3 Rene Descartes (1596 - 1650)
"I think (drink) therefore I am, but I don't know about you guys"
Everyone who has been to university bar with a group of drunken friends has heard this one before. "How do I know you are real. You could all be part of my imagination. I might wake up from a dream and you will disappear".
Also rejected the role of authority, but choose mathematics and deductive reasoning as the basis for his approach to science. He refused to accept any belief unless he could "prove" it. He used his famous "I think therefore I am" to "prove" his own existence, and then went on to "prove" the existence of God. For those who are interested, one of Rene's proof goes something like: I can imagine perfection, and God is perfect. To not exist would be an imperfection, therefore God exists. Hmmm.
2.4 Immanuel Kant (1724 - 1804)
The following is part of a translation of Immanuel Kant's "The Critique of Pure Reason" [6]
"all our intuition is nothing but the representation of phenomena; that the things which we intuite, are not in themselves the same as our representations of them in intuition, nor are their relations in themselves so constituted as they appear to us; and that if we take away the subject, or even only the subjective constitution of our senses in general, then not only the nature and relations of objects in space and time, but even space and time themselves disappear; and that these, as phenomena, cannot exist in themselves, but only in us. What may be the nature of objects considered as things in themselves and without reference to the receptivity of our sensibility is quite unknown to us"
This could have been written by Niels Bohr 150 years later. Kant was, of course, not attempting to understand the meaning of a new and strange theory; he was discussing the limits of human knowledge. In Kant's day it was not uncommon for philosophers to make meta-physical assertions and arguments like Descrates' "Proof of the existance of God". In modern language, Kant pointed out the difference between the internal mental models we build of the external world, and the real objects themselves which we know only through our senses. We can apply logic to our mental models, "whilst the transcendental object remains for us utterly unknown".
It is a measure of the success of Kant's view that arguments such as Descrates' would today be meet with howls of derision. The division between Science and meta-physics is now clearly established; Science relates to that which we can intuit through our senses, meta-physics and religion relates to that which we cannot.
2.5 Positivism (early 20th Century)
Positivists take Kant's position even further; they reject meta-physical statements as utterly meaningless. Religion, for example, is excluded from philosophy. Positivists regard a statement as meaningful only if it can be verified. Statements can be verified if they are experimental propositions, or if experimental outcomes can be deduced from them. Experimental propositions are judged as verified if they are probable based on experimental evidence.
Positivism clearly influenced the Copenhagen interpretation: Only those "properties" of a quantum system that can be measured, or manifest themselves in measurable quantities, are meaningful. (Measuring devices take the place of Kant's "senses").
2.6 Niels Bohr (1885 - 1962)
Bohr was not a philosopher, rather like Galileo, he was a scientist. Bohr is forever linked with the Copenhagen Interpretation which he was largely responsible for. Bohr produced one of the first quantum models of the atom, engaged Hiesenberg and others in debate over the nature of Hiesenberg's work, and defended the Copenhagen Interpretation against attacks by Einstein.
2.7 Sir Karl Popper (1902 - 1993)
Scientific enquiry was regarded as primarily inductive in nature up until this point. Popper's view was that scientific theories are axiomatic structures which are subject to falsification. i.e. they cannot be proved correct, but they can be proved incorrect. Science is viewed as a producing a series of theories which are better and better approximations to the "truth".
2.8 Thomas Kuhn (1922 - 1996)
Placed science in a social context. Kuhn was sceptical of the Popper's idealistic view of how scientists work. Scientists are mostly problem solvers, working within the scope of an all encompassing and highly successful theoretical structure, or paradigm, such as Newtonian Physics, or General Relativity, or the Central Dogma of Molecular Biology. Few venture outside the framework, spending most of their time applying the rules of the paradigm to the problems they have to solve. Only occasionally do "revolutions" such as Relativity or Newtonian Physics come along and change the paradigm. The idea that Science "reveals" the truth is rejected.
"A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it." - Max Plank (Authbiography)
Kuhn regards Science as a social endeavor, but does not explain the precise mechanisms by which new scientists make probability judgments about the "correctness" of theories.
2.9 George Polya (1887 - 1985)
Laplace, Cox, Polya and others have placed "plausible reasoning" (i.e. reasoning using probability) at the heart of not just scientific thinking, but all of human reasoning. Polya has analysed scientific advances to show the operation of probability syllogisms.
Bayesian probability provides a framework for understanding previous ad-hoc attempts at codifying scientific endeavours. Popper and Kuhn's description of scientific thinking is incomplete. Scientific theories are indeed axiomatic structures capable of falsification, but new experimental evidence often fails to convince. Belief in theories is more robust than Popper would expect; there is almost always some experimental evidence which contradicts even the most successful of theories, but scientists make probability judgment about the correctness of theories and evidence.
"It is more important to have beauty in one's equations than to have them fit experiment ... because the discrepancy may be due to minor features that are not properly taken into account and that will get cleared up with further development of the theory ... It seems that if one is working from the point of view of getting beauty in one's equations, and if one has really a sound insight, one is on a sure line of progress" - P.A.M. Dirac.
2.10 Kant and Copenhagen
Copenhagen is unique amongst Quantum Mechanics interpretations in that it is firmly routed in classical Western philosophy. The Kantian world-view is show in the diagram below. Information makes its way from the external world into our consciousness via our senses. We use that experience to construct mental models that predict the behaviour of the external world. If the models are good ones, it becomes easy for us to forget that we are only reasoning with mental constructs and the true nature of the external world is hidden from us.
The Copenhagen world-view is shown in the diagram below. The similarity is striking. Information flows from the external world through "measuring devices". Quantum Mechanics goes further than Kant: it tells us what characteristcs of the measuring device are important, and how to reason with the results. It tells us that Kant's world view does not require consciousness, only "intellegence" - a computer will do ever bit as well as a conscious being. It tells use we need to select a Classical-Quantum boundary - i.e. a set of measuring device which the intellegence uses to interact with the world.
Hidden variable theories and virtual all alternative interpretations attempt to understand Quantum Mechanics in terms of classical "wheels and cogs" (fields and particles). The universe is a machine; the job of Physics to accurately describe those wheels and cogs and the wat they interact. There is no reason why there should be any limit to our understanding. Unfortunately Heisenberg begs to differ.
3. Paradoxes, Phenomena and Proofs
3.1 The Waveform that refuses to collapse - The Measurement Problem
The Measurement Problem: Suppose, for consistency, we decide to treat the
measuring device as a quantum device, then the waveform associated with any
experiment never collapses!
This is not too hard to see. Suppose we have a radioactive source which has a
50-50 chance of emitting a particle within a given time frame. We set up a
quantum measuring device to detect the possible emission of a particle. At the
end of the specified time, the waveform describing the measuring device is
in a state which is a 50-50 mix of "particle detected" and "particle not
detected"! i.e. ( |detected@1> + |not detected@1>)/Ö2
We can attempt to set up a second measuring device to extract the measurement from the first measuring device. It too is a quantum system so after the experiment we find it is still in a 50-50 state:
In fact it is possible to add an infinite number of cascaded measuring devices but the waveform stubbornly refuses to collapse. i.e. it is always in a mixed state.
The Measurement Problem is at heart of many interpretations of Quantum Mechanics. What makes the waveform collapse? This is what the various interpretations have to say.
4.1.1 Copenhagen Interpretation
What is this waveform collapsing rubbish? Remember the waveform is a mathematical construction only used to predict the probability of outcomes for a specific experiment. It does not "collapse" since it is not real and does not have any meaning outside the context of the original experiment. Asking "What makes it collapse?" implies both reality (whatever that means) and a lifetime greater than the original experiment. Anyway, it is improper to regard a measuring device as a quantum device. Copenhagen draws a distinction between the quantum system and the measuring device (the Quantum-classical boundary).
3.1.2 State Vector Interpretation
Don't know, it just does, umm, when it interacts with the measuring apparatus. To avoid having to answer this question the State Vector Interpretation raises the collapse of the waveform to the status of an axiom. It should be noted that in its standard form, State Vector Interpretation does not specify EXACTLY when the waveform collapses which leads to ambiguity (Wigner's Friend). I.e. State Vector Interpretation is incomplete.
3.1.3 Consciousness Causes Collapse
For consistency, all devices should be treated as quantum devices, however we know when we "look" at the outcome of an experiment we always see an outcome, i.e. the waveform has collapsed.
Suppose we consider a simple electron position measurement experiment. We know the waveform does not collapse when the quantum measuring device initially "measures" the electron's position. We know the human eye can also be considered a quantum system, so the waveform does not collapse when photons from the measuring device interact with the eye. The resulting chemical signals in the brain also can be viewed as a quantum system so it is not responsible for the collapse of the waveform. However a conscious observer always sees a particular outcome. i.e. the waveform collapse can be traced back to it's interaction with the consciousness of the observer!
Perhaps a human observer causes the collapse of wave functions, but what about a parrot, or a bacterium? Did the Universe behave differently before life evolved?
3.1.4 Hidden Variable Theories
Measurement does just that. It reveals the values of underlying quantities (usually, although this depends on the theory). Until the more sophisticated theory underlying Quantum Mechanics is discovered it is not possible to make any definitive statements. Individual theories can be tested against experiment and the current formulation of Quantum Mechanics but failure of a specific theory does invalidate the quest for a such a theory.
3.1.5 Many Worlds Interpretation
All the different possibilities happen, each in a separate "parallel" universe. I.e. There are at least 2 parallel universe, one with the particle emitted and detected and one were it has not.
3.1.6 Consistent Histories
A sample space (framework) needs to be defined before any analyse is done. In the case above, a suitable choice would be
There is no infinite regression of measuring devices. The choice of framework creates a Quantum-classical boundary. Once an observer chooses to restrict his information to that provided by the framework, he enters the classical domain. The probability of these events can be manipulated using standard probability theory. I.e. the events can be treated as "real". A quantum measurement become indistinguishable from a classical measurement.
3.1.7 Decoherence
Decoherence is a vague term applied to situations where "the interference of waveforms is suppressed". It has become an increasingly popular concept in recent years, particularly since understanding the technical aspects of decoherence is essential to the construction of quantum computers.
Despite what many science magazines and websites say, decoherence does not resolve the measurement problem. The argument presented goes something like: "In the real world, quantum systems interact with an external environment. The result of such interactions is that the waveform describing the combined system rapidly moves toward stable, environmentally selected "pure" eigenstates. In particular, a measuring device can be regarded as part of the extremely environment; interaction with the measuring device causes the combined system to move towards eigenstates characteristic of the measuring device." However this is a long way short of solving the measurement problem.
Since decoherence does not solve the measurement problem, it does not help explain "how the macroscopic world emerges from the quantum world".
The term decoherence is also used in the Many-Worlds interpretation to indicate the selection of a universe, and the separation of a superimposed state into the "pure" states associated with each universe.
3.2 Schrodinger's Cat
Synopsis: Schrodinger published the following paradox in 1935. A cat is placed in a box for a period of time with a radiation source. During that time there is a 50-50 chance of a particle will be emitted by the radiation source and be detected. If it is detected, a poisonous gas will be released killing the cat. Just before the end of the experiment, the quantum mechanical wave function describing the cat is a 50-50 mix of live and dead cat. The cat is in a state which is half alive and half dead!
This paradox highlights the status of the waveform. Is it "real"? This is discussed in more detail in Wigner 's Friend.
3.3 Wigner's Friend
Wigner (1961) asks his friend to watch an experiment for him and leaves. When he returns he asks his friend what the result of the experiment was. If he views his friend as part of the experiment and therefore a quantum system, the total system is in a indeterminate state until he asks his friend for the result of the experiment. However, his friend is certain that he was not in an indeterminate state prior to Wigner 's enquiry!
This is really a version of Schrodinger 's cat with a talking cat.
Note that Wigner 's friend could be replaced by a simple recording device. In this case we would have no trouble imagining the recording device waveform in an indeterminate state without any paradox arising. It is often stated that this paradox highlights that consciousness must be given special treatment in Quantum Mechanics!
How do the different interpretation handle this "paradox"?
Copenhagen interpretation
The waveform has no reality and so has no effect on any friend or cat. There is no paradox.
State Vector Interpretation
If the friend is viewed as part of the quantum system, he is indeed in a indeterminate state with respect to Wigner ( i.e. Wigner does not know how his friend will answer) and waveform collapse will occur when his friend answers.
If his friend is viewed classically (i.e. he is not part of the quantum system), the waveform collapses when his friend observes the experiment.
If the waveform is "real", then it is reasonable to assume that the waveform "really" collapses only once for all observers at the same point in space-time.
The paradox arises because the first part of the argument assumes that the friend is part of the quantum system, and the second part of the argument assumes that his friend is not (i.e. he is a classical observer). The paradox is resolved if all observers agree on common (and correct) conditions for waveform collapse. State Vector Interpretation does not attempt to specify the conditions under which collapse occurs and so State Vector Interpretation is incomplete (and therefore unsatisfactory).
Consciousness Causes Collapse
Consciousness Causes Collapse = State Vector Interpretation + waveform collapse when the waveform encounters consciousness. Since Wigner's friend is a conscious being, the waveform collapses once he (or she) interacts with the experiment. There is no paradox, however Consciousness Causes Collapse suggests that standard Quantum Mechanics (Wigner's friend is in a superimposed state) is wrong.
Many World Interpretation
The Many-Worlds Interpretation has the same issues as State Vector Interpretation, with "selection of our Universe" replacing "waveform collapse. The Many-Worlds Interpretation does not specify the conditions under which selection of our Universe occurs and so it incomplete. Variants abound - e.g. it is possible to combine Many-Worlds Interpretation with Consciousness Causes Collapse so that our Universe is selected once a conscience being interacts with an experiment.
Oops!
One wonders what happens if Wigner walks away and falls into a black hole. The waveform would never collapse! If the waveform is "real", the system would remain in a indeterminate state forever?!
3.4 EPR
Although Einstein was one of the founders of Quantum Mechanics, he was unhappy with many aspects of the theory and famously remarked "God does not play dice". Initially Einstein attempted to show that Quantum Mechanics was inconsistent by showing that it was possible to circumvent HUP. He was not successful and abandoned that approach in favour of attempting to show Quantum Mechanics is "incomplete". The result was a paper published with the Podolsky and Rosen (EPR) that, in the authors opinion, did a pretty good demolition job on a great many interpretations.
An EPR experiment, shown below, involves any two entangled particles (e.g. photons, electrons etc) emitted from a single source.
EPR Apparatus
The Minkowski diagram below shows the world line of two particles (purple) moving outward from O. The first measurement is made at A. The diagram show 2 frames of reference, a "stationary" frame shown in black, and a "moving" frame shown in red.
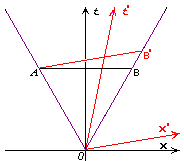
EPR Minkowski Diagram
The waveform associated with the emitted particles is in a mixed state (i.e. properties are not well-defined) until the first measurement in made at A. Conservation laws require that the two particles have opposite momenta/spin, so the first measurement at A causes the waveform of the second particle at B to collapse also. Information about the result of the measurement at A propagates instantaneously (faster than light) across space to other entangled particle! EPR argue this shows either Quantum Mechanics is a "non-local" theory (relies on faster-than-light propogation of information), or "incomplete" since it does not describe the mechanism used to maintain momenta/spin conservation.
The argument is sharpened by considering an observer at B' who is moving with a constant velocity with respect to the observer at B. Relativity denies the concept of simultaneity - if the waveform is real, then (presumably) the waveform collapses for everyone at the same points in space-time. However an observer at B believes the waveform collapses before the observer at B' sees the measurement at A ! The instantaneous collapse of the waveform requires us to choose a preferred frame of reference!
Does collapse occur along the space-like surface AB or the space-like surface AB'? Or along some other space-like surface?
What do the various interpretations say?
Copenhagen interpretation
The waveform is not "real", is observer dependent and linked to a specific experiment. The initial waveform associated with observer A initially does not indicate values for momenta/spin for either particle. Once a measurement is made at A, a new waveform is associate with observer A which indicates the new measured value of momenta/spin, AND the values of momenta/spin of the particle at B implied by conservation laws.
Although observer A now knows the momenta/spin of the second particle at B, it cannot communicate this to observer B. Observer B in unaware of observer A's waveform, and his waveform does not indicate the values for momenta/spin measured at A. If he chooses to measure some property then the value obtained will be that demanded by any relevant conservation law, but otherwise random.
Since the separate waveforms do not interfere with each other (they are not "real"), there is no problem.
EPR were correct: Quantum Mechanics is incomplete in the sense that it does not describe the mechanism that "enforces" conservation laws (or the underlying symmetries), however Quantum Mechanics is complete in the sense that no other description is possible.
State Vector Interpretation and other Real Waveform Theories
EPR poses serious problems for the State Vector Interpretation.
EPR shows that the State Vector Interpretation is incomplete AND non-local. It is this incompleteness however that prevents further attacks. The State Vector Interpretation does not specify collapse criteria.
Many World Interpretation
EPR poses even more serious problems for Many-Worlds Interpretation since there is less weasel room.
Many-Worlds Interpretation implies that the entire Universe splits into multiple copies of itself when the entangled particles are emitted. The moment the first measurement is made, a particular universe is selected. Does this selection process occur along the space-like surface AB or the space-like surface AB'? Or along some other space-like surface? (Universe selection = waveform collapse) The Many-Worlds Interpretation does not have a get out-of-jail card - selection of a Universe has or has not occurred at any point in space-time.
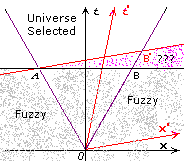
EPR/Many-Worlds Interpretation Minkowski Diagram
EPR definitely shows that Many-Worlds Interpretation is non-local AND incomplete. It requires some definitive mechanism to determine the boundary between the fuzzy pre-selection soup of possibilities and the selected universe.
Can EPR be used as a basis for faster-than-light communication?
No.
Suppose a source that generates particle pairs with random "coupled" spin is placed halfway between the earth and the moon. Even if measuring the spin of a particle arriving on the earth instantaneously causes the waveform "to collapse" on the moon, it is still not possible to detect that collapse since the actual measured values are randomly distributed!
Reality
The EPR paper contained an interesting definition of reality:
"If, without in any way disturbing a system, we can predict with certainty (i.e. with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity"
After the measurement of a particles position it's momentum is not well defined. I.e. it's value cannot be determined with probability equal to unity. According to the definition there no longer exists an element of physical reality corresponding to the particle's momentum.
The "unreality" of a particles position and momentum is a consequence of HUP and a particular definition of reality! For any property X of a quantum system, there is (nearly) always another property Y which is complementary to X and so we are lead to the conclusion that no particle has any permanently "real" properties!
Comment
EPR is one of the most persuasive arguments in favour of the unreality of the waveform.
What role does "information" plays in Quantum Mechanics? There are 2 particles, but because of conservation laws, their momenta/spin is described by a single "bit" of information. A measurement provides the value of that bit of information. It does not matter which particle is measured first. In fact, it has already been noted that which particle is measured first depends on the observer's frame of reference. Relativistic arguments make it questionable whether that the idea that an influence "travels" superluminally between the particles makes sense.
3.5 Von Neuman's Impossibility Proof
This theorem states that no hidden variable theory is consistent with Quantum Mechanics. At the time of publication it seemed that this proof sealed the fate of hidden variable theories, however this is now disputed by some authors. Criticisms of Von Neuman's Impossibility Proof are generally very technical in nature. Bell's Inequality below is simpler to understand and possibly "does the job better" where the job is to discredit hidden variable theories by imposing very stringent conditions on them.
3.6 Bells Inequality
In 1964, Bell published a paper containing his famous inequality. If a system consists of an ensemble of particles having three boolean properties (observables) A,B and C, then classically the probabilities associated with selecting particles with various properties obeys Bell's Inequality.
| Bell's Inequality: P(A, ¬B) + P(B, C) ³ P(A, C) |
Bells Inequality can be seen by examining the Venn diagrams below. The LHS shows the sets A Ç ¬B (pink) and B Ç C (green). The RHS shows the set A Ç C.
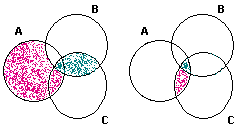
Bells Inequality also applies to Hidden Variable theories - the set of states can be modelled by the same Venn diagram; A (set) now represents the set of states that would yield a positive result if a measurement of (observable) A were made, before any measurement of B or C.
The problem with applying the inequality to Quantum Mechanics is that measuring one quantity may affect the measurement of another - it is generally not possible to measure the initial values of both A and B for a single particle. However, entangled particles give us two bites of the measurement apple. Suppose we have an EPR style apparatus and
- there is a reciprocal relationship between the values of measurement of A on the two particles. I.e. there is a conservation law that allows us to predict the value of a measurement of A on one particle given knowledge of the outcome of a measurement on the other.
- the same type of relationship exists between the particles with respect to quantity B.
- the value of A is measured for one particle and found to be a,
- the value of B is measured for the other particle and found to be b.
The "first" particle must havestartedwithstate(A=a,B=¬b).
Common sense would indicate that Bells Inequality must be true, however it turns out that Quantum Mechanics does not obey Bells Inequality.
3.6.1 Example
An EPR style apparatus emits entangled photons that then pass through separate polarization analysers (See figure 2 below). Let A, B and C be the events that a single photon will pass through analysers with axis set at 0o, 22.5o and 45o to vertical respectively.
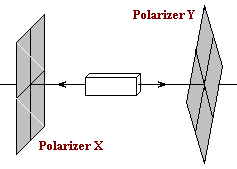
|
EPR style polarizer setup. |
P(X, ¬Y) = probability that a photon will pass through an analyser X but not analyser Y. According to Quantum Mechanics, P(X, ¬Y) = ½ sin2(angle between analysers);
We use the version of Bell's inequality obtained by putting C ®¬C (also easily proved with Venn diagrams).
[Bell's Inequality] P(A, ¬B) + P(B, ¬C) ³ P(A, ¬C)
Þ ½ sin2(22.5o) + ½ sin2(22.5o) ³ ½ sin2(45o)
Þ 0.1464 ³ 0.25
which is obviously nonsense. i.e. Quantum Mechanics is inconsistent with Bell's Inequality.
Experimental evidence supports Quantum Mechanics, not Bells Inequality. Did anyone seriously believe that Quantum Mechanics, one of the most accurate and successful theories of all time, is incorrect in this simple case?
3.6.2 Conclusion
Bells Inequality shows it is not possible to simply view particles as having properties attached to them in a classical manner - otherwise Quantum Mechanics would be forced to obey Bell's inequality which it does not. If property A is measured, it is not sufficient to say that the value of B is no longer known; it is no longer possible to say that any value of property B is associated with the particle.
Quantum Mechanics does not support a "locally real particle model". Successful hidden variable theories will have to sufficiently sophisticated to take this into account.
3.7 Closed System Waveforms
The Universe is a closed system. By definition there can be nothing outside it.
Quantum Mechanics has become an integral part of Cosmology; the entire Universe is treated as a quantum system. What does the waveform describing the evolution of the entire Universe look like? Here's what the various interpretations say.
3.7.1 State Vector Interpretation
When does the waveform collapse? The State Vector Interpretation is incomplete; different variants have different collapse criteria. Those variants that specify that collapse occurs as a result of external measurements requires a measurement external to the entire Universe before collapse can occur! Quantum waveforms exhibit symmetry so post-poning collapse has consequences: the Universe would exhibit similar symmetry until collapse occurs.
3.7.2 Consciousness Causes Collapse
The waveform cannot collapse until it encounters an external consciousness!
3.7.3 Copenhagen Interpretation
The waveform only describes the probabilities. At some point the experimenter must decide what the experimental outcomes are, in which case he creates a Quantum-classical boundary. The waveform described the evolution of the Universe prior to the designated outcomes. There are no issues associated with this interpretation or any of it's variants
3.8 Consciousness
A number of well respected scientists have conjectured that it may be possible to explain consciousness using concepts from Quantum Mechanics. Typically consciousness is equated with "quantum tunnelling" across synaptic clefts and the like. The problem with all such attempts to reduce consciousness to particular type of event within the brain is that the same events typically happen outside the brain. For example, if consciousness is the result of quantum tunnelling in the brain then if quantum tunnelling occurs outside the brain, say inside a radar gun, does the radar gun become conscious? Luke, perhaps the rocks and trees and air some sort of low level consciousness they do indeed have.
There are alternatives.
It is sometimes claimed that consciousness magically appears once a system's complexity grows beyond a certain point. That's wishful thinking. The idea can be challenged on a number of grounds - it is possible to point to many extremely complex systems which display no indication of consciousness (e.g. telephone networks, a kidney, the Internet), and a broken complex systems (e.g. large software systems) can be just as complex as an unbroken system but may be rendered useless by a single flaw. Proponents usually patch up the hypothesis by the addition of arbitrary criteria for distinguishing those systems that might be conscious from those that clearly are not (The addition of ad-hoc criteria is very reminiscent of the situation with respect to waveform collapse)
Another possibility arises from work on artificial intelligence. Rodney Brooks suggests that the "Universe is it's own best representation ". Brooks' approach is to build robots that simply process the information presented by sensors to do very specific 'simple' jobs. An robot insect might respond to light or noise by behaving in a certain way (e.g. turn away from the light or noise, or lunge at "food"). The result can be surprisingly complex and apparently intellegent behavour - but the intellegence (consciousness?) is a result of both the robots reflexive actions and its external environment.
There is some support for this hypothesis. Animals, driven by "instincts", display caring behaviour towards their offspring, however the mechanical (?) nature of this care can be exposed in unusual circumstances. Birds, for example, may refuse to feed hatchlings if they fall out of the nest. The hatchlings may only be inches away from their siblings but the parent bird will simply ignore them. It would be interesting to know how much human behaviour is really of this kind.
A robotic vision system built on Brook's principle might consist of a number of simple systems (edge enhancement, stretch / match current image against image library etc). Most alternative approaches attempt to construct a complete "wire-frame" internal model of the universe, and identify features by matching sensory data against the model, but this has proved extremely difficuly to do. The attraction of the internal model approach is that once the model has been constructed and "matched" against the real world, information such as facial features can be easily extracted from it.
Humans however don't seem to need a mental model of a human, or even an animal, to identify facial features. Humans see faces everywhere from cars to the Mars, suggesting that the part of the brain that identifies faces operates directly on (possibly pre-processed) sensory input, as per Brooks, and does not use an internal model. Internal models are also fragile; they attempt to reduce the world to abstract concepts familiar to programmers and mathematicians such as sets, logical propositions etc. An internal model of a person may include "slots" for two legs. It may work wonderfully 99% of the time. It may even handle amputees. But would it handle Jake the Peg? Furthermore, if a system is based on logical inferences, the consequences of a mistake can provoke a massive storm of revisions. Brooks' systems use the fact that constraints are modelled implicitly in the data from the real world - systems that process that data continue to work even if there are radical changes to the environment (but potentially give the "wrong" result). Developmental Psychology favours Brooks: human babies are almost totally dependent on sensory input and only gradually relinquish that reliance. (E.g. take 2 fat glasses of Orange Juice filled to the same height. Ask a 4 year old "which has more?". Now pour one of the glasses of Orange Juice into a tall thin glass. Ask the 4 year old now "which has more?") It is typically not until late adolescence that humans are fully prepared to use logic to override their senses. (See Jean Piaget)
Brooks approach is fascinating since it implies that intellegence cannot be localised into a "machine", it is also a function of the external universe it interacts with. So far the approach has only been applied successfully to insect-like robots. If Brooks is correct and the "Universe is it's own best representation", intellegent systems cannot exist without a deep connection with the external world. True artificial intelligence requires not a disembodied logical machines like HAL 9000 in "2001 - A Space Odyssey", but something more reactive with capabilities akin those of the artificial humans in the "The Stepford Wives".
However intellegent behaviour is not consciousness, yet human consciousness and its corresponding sense of purpose is unimaginable without some form of intellegence.
What is the link between consciousness and perception?
There are limits to what can be described by language and therefore Physics. Physicsts can state with certainty that yellow light corresponds to a specific frequency range, but such a description is incapable to transmitting the experience of Yellow. The true essense of Yellow has to be experienced.
Consciousness is not well understood or easy to define. Whatever it is, it is possible that it is not "a single thing", and it may not reside in any identifiable part of any system. It is even possible that consciousness has no explanation. It might just 'be'. To equate it with any Quantum phenomena is probably naive.
3.9 Do hidden Variable Theories have any value?
HUP ensures that Hidden Variable Theories (probably) cannot be used to generate more accurate experimental predictions than standard Quantum Mechanics without conflicting with it while adding extra layers of unverifiable complexity. Einstein is reputed to have referred to at least one such theory (Bohm's) as an "unnecessary superstructure". It is also known that any Hidden Variable Theory must also have "unsatisfactory" features such as non-locality which removes some of the motive for looking Hidden Variable Theories in the first place. Do they have therefore value?
Occam's Razor would suggest not, but...
There are at least 3 circumstances where a Hidden Variable Theories may add value. (1) A Hidden Variable Theory could be so simple and elegant it could become compelling, even if it could never be verified, but Bell's Inequality and Von Neuman's Impossibility Proof would ensure that it would not be a simple particle model. (2) Since a successful Hidden Variable Theory would give the same experimental predictions as standard Quantum Mechanics, such a theory could prove useful as a calculation methodology. Computer programs are deterministic and can approximate Quantum Mechanics system to any desired degree of accuracy given sufficient computing resources) (3) A Hidden Variable Theory may be able to explain features of Quantum Mechanics that standard Quantum Mechanics cannot, for example, predict the value of coupling constants. This is probably the only case when a Hidden Variable Theory could generate more accurate values than standard Quantum Mechanics. (Although it could only ever be verified to the same level of accuracy as Quantum Mechanics!)
So far no-one is close to producing a Hidden Variable Theory to rival standard Quantum Mechanics. (That includes Bohm)
Hidden Variable Theories also have philosophical implications.
3.10 Is there free will?
Copenhagen views the world as inherently unpredictable. There is room for "free will" since the future is not known with certainty. It could be that an observer "plays dice" with God. It is also possible however that the Gods have, like the characters of a Greek tradegy, pre-ordained our fates. Copenhagen is essentially a postivist interpretation. Issues of "free will" are meta-physical considerations. Copenhagen has nothing to say.
Hidden variable theories, on the other hand, imply a clockwork universe wound up by God at Creation and unfolding in a predetermined way. There is no true randomness, only a lack of knowledge of initial conditions. All of human history was pre-ordained from the beginning of Time. The world is not random, merely chaotic.
But experiment can never tell the two option apart.
3.11 Probability - Frequentists vs Bayesians
Probability theory as a branch of mathematics is several hundred years old. It would be expected that probability theory is a stable, well understood branch of mathematics, perhaps with a small number of outstanding complex problems. But this turns out not to be so. There is a schism within Probability theory which almost exactly matches the schism within the Physics community over Quantum theory. There are two main camps: Frequentist and Bayesians, while the great mass of practioners follow Feynman's dictum "Shut up and calculate" [1a]. Both approaches (generally) give the same results, although one approach may be significantly simpler than the other.
Frequentists consider that probability to be essentially about "frequencies"; probabilities describe the long term likelilhood of an event. Frequentists believe that one of the goals of probability theory is to "correctly" estimate the "propensities" (Popper) of a physical system. Probabilities are objective. For example, if a coin is fair, then the propensity (probability) of getting a Head when the coin is tossed is 0.5.
Bayesians believe that probability describes the degree of belief in a proposition. Bayesians regard a probability of 0.5 of getting a Head as meaning that there is no reason (information) to expect one outcome over the other. For Bayesian, probability is subjective. Different observer have different information and therefore may assign different probability to the same propositions. Bayesians deny there is any instrinsic probability associated with physical events alone. Jaynes [5] systematically destroys any notion that it makes sense to assign a probability based on the physical properties of the coin. For example, he explains that with a little practice it is possible to consistently toss Heads even with a "fair" coin.
There are problems with the frequentist approach. For example, what does it mean to say: "The probability of rain tomorrow is 30%". The event is a one-off. It cannot be re-run. So how is it possible to talk about any frequency? The notion can be saved but at the expense of moving rapidly away from the original simple notion. There are many examples where the notion of probability is divorced from frequency. In financial markets, probabilities do not reflect "real" propensities (no one knows what the market will do) but an extensive literature has been developed which uses probability theory to value financial products. These probability measures reflect a "market view".
The frequentist position has been the orthodox position during much of the 20th Century, possibly because it more closely reflects the standard mathematical treatment of probability (Kolmogorov Axioms, random variables etc). The goal of the axiomization of probability theory however is to ensure mathematical consistency. It does not follow that the standard axiomatic treatment best refects the best understanding of what is "going on" when probability is applied in the real world.
We shall adopt Bayesian notation without comment. For example,
[1a] Apparently actually attributable to P.A.M. Dirac.
3.12 The role of probability in Quantum Mechanics
The Bayesian position seems a good fit with the Copenhagen interpretation of Quantum Mechanics, but surely Quantum Mechanics also produces objective probabilities. For example, the probability that a photon will be emitted must be independent of the observer. Paradoxes such as Wigner's Friend clearly show that this is not the case; Quantum Mechanics produces subjective probability measures. Different observers
3.13 Feynman's Rule
These rules underlie the calculation of probabilities in modern quantum theories such as QED.
Classical probability theory: If A and B are mutually exclusive events, then
Feynman's probability rules : (taken from 1-7 of The Feynman Lectures on Physics) "The probability of an event in an ideal experiment is given by the square of the absolute value of a complex number YA, which is called the probability amplitude"
"When an event can occur in several alternative ways, the probability amplitude for the event is the sum of the probability amplitudes of each way separately. There is interference."
"If an experiment is performed which is capable of determining whether one or another alternative is actually taken, the probability of the event is the sum of probabilities of each alternative. The interference is lost"
A similar rule applies to the conjunctions of independent propositions:
Example: The diagram below shows a classic double-slit diffraction experiment. Let A be the proposition "The particle goes through slit A" and B be the proposition "The particle goes through slit B". The various possible alternative ways an event can happen are sometimes called "histories". I.e. A and B are alternative histories. Feynman's rules correctly describes double-slit diffraction.
Double Slit Diffraction
But what does it mean? Bohr: The relationships between alternate "possibilities" actually are statements about the experimental apparatus and its symmetries as much as they are about the measured external world. (TODO)
3.14 Feynman's Sum of Histories
Feynman diagrams are used to analyse particle interactions. The initial and final states are determined, and diagrams are "drawn" for each possible interaction leading to the desired outcome. During these interactions, "objects" can do whatever is possible, and do. Photons, for example, routinely travel faster or slower than the speed of light. Virtual particles are created and destroyed. Each unique topology + choice of coordinates for events (i.e. graph vertex) yields a possible history. Summing the amplitudes over all possible histories yields the probability of the original interaction.
The Feynman formulation is fundamental to modern theories such as QED and QCD, however there are technical problems. The sum of Feynman histories for an given particle interaction can be infinite. Results can still be obtained by use of "Renormalisation" however the process is mathematically dodgy. (Basically just stopping counting at some level of diagram complexity and "adjust" the numbers so the known values match with experiment) Some physicists attribute this failure to the process of summing diagrams down beyond the Planck length (10 -33 cm). Despite problems, the Feynman approach is stunningly successful. e.g. the QED calculation of magnetic moment of an electron agrees with experiment to within one part in 108.
4. Conclusion
Interpretation |
When does waveform collapse occur? |
| Copenhagen Interpretation | Waveform collapse is nonsense. |
| State Vector Interpretation | Waveform collapse criteria not specified ("Roll your own"). |
| Consciousness Causes Collapse | Waveform collapse is the result of interaction with consciousness. |
| Hidden Variable Theories | Waveform is incomplete view of underlying "classical" theory. Many variants - collapse critieria not specified. |
| Feynman's Sum of Histories | Not an interpretation - makes no statement regarding collapse - computation methodology only. |
| Many World Interpretation | Many variants. Waveform collapse = selection of Universe. Collapse criteria not specified. Incomplete. |
| Extended Probability | Copenhagen variant. Waveform collapse is nonsense |
| Consistent Histories | Interaction with the measuring device causes decoherence. Real waveform? |
The various interpretations arise from the different ways of answering some fundamental questions. See flowchart below.
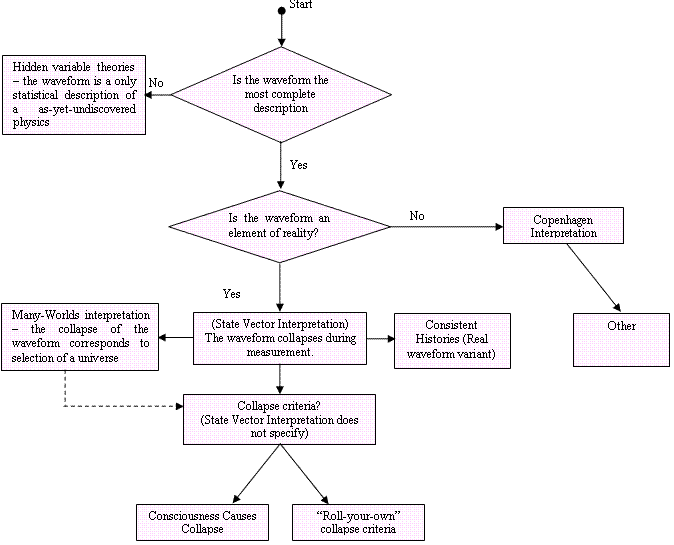
It seems to me that:
-
All real waveform interpretations (Many-Worlds Interpretation, State Vector
Interpretation, Transactional Interpretation, etc) have serious problems with
EPR. They are (in my opinion) not viable.
-
Only the Copenhagen Interpretation is
viable.
-
The Many Worlds Interpretation is a bit of a cop out. It identifies the sample
space of any experiment as "real" by playing semantic games with the meaning of
the term. It does not contribute to the understanding of how and when the
waveform collapses (= how and when our "universe is selected").
-
Consciousness Causes Collapse has trouble specifying exactly what constitutes
consciousness.
My own personal view is that Consciousness Causes Collapse is a really a distraction - it's a consequence of failing to follow Copenhagen. Copenhagen says that you must select a quantum-classical barrier. Consciousness Causes Collapse results from refusing to do that, tracing the measurement process backwards and finding that a quantum-classical barrier must exist somewhere. The quantum-classical barrier is then chosen to be in the last possible place - the mythical interaction of the qauntum world with consciousness (presumed classical).
- The Copenhagen Interpretation is pretty much trouble free. Many of the original statements are a bit vague and dated, but much of Bohr's intuition survives, surprisingly, in some of the statements of alternative interpretation such as Consistent Histories.
5.Time
5.1 Clocks
A measurement of time requires a clock. What is the best way to build a quantum clock? How do real clocks work?
The diagram below shows a classical pendulum clock with q as the angle between the pendulum and vertical, the pendulum has length R and mass m.
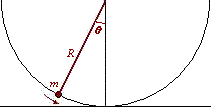
The system has only a single state variable q, and conjugate momentum p. Classically time is measured by continually tracking q, and counting the number of times the pendulum crosses the vertical (i.e. the value of |q| = 0). If a single oscillation is missed, the clock becomes inaccurate. In a corresponding quantum system, HUP implies that any accurate measurement of q would result in large uncertainty in p. It would not be possible to continually track the motion of the pendulum. q would then vary randomly, not regularly as required for the device to qualify as a clock.
Perhaps an atomic clock would be a better bet to scale down to the quantum domain? Atomic clocks use precisely known energy lines to frequency lock microwave radiation; very fast electronics count wave crests of millions of photons in a powerful oscillating field. Atomic clocks won't work with a single photon; they are really classical devices that cannot be scaled down. They only provide a statistical estimate of the time; they do not measure time. How do we know there is a difference between the two concepts? Classically the distinction is blurred, but in Quantum Mechanics measurements are exact. Two different measuring devices which both measure the momentum of a particle must give the same value. Two devices which give statistical estimates are free to produce different values. In fact, no measurement can be taken as accurate since it is always possible to build a "more accurate" (higher confidence) device.
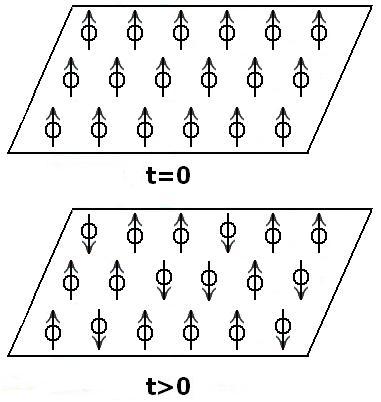 |
| The device consists of a large number of particles all prepared in identical states. A statistical of estimate the time past since the assembly of particles was prepared (t=0) can be made by counting the number of particles that have changed state. A clock can be designed with arbitrarily high confidence by increasing the number of particles. It is however not a measurement of time. |
It turns out all known systems are equally unsuitable, and the failure to create a quantum clock is not just due to a lack of imagination.
5.2 Pauli's Theorem
Pauli's Theorem: The existance of a self-ajoint operator conjugate
to the Hamiltonian implies a continuous Hamiltonain spectra spanning all of ![]() .
.
Translation: There is no such thing as a time (measurement) operator in Quantum Mechanics. There is no time operator T such that T|Y> = t|Y> for all states |Y> where t is "the time".
At first this appears shocking, but it is not so surprising in retrospect since
-
Quantum Mechanics deals with observables - to measure time it is necessary to
have a device to do so. A system does not automatically include a clock, so a
description of the quantum system will not necessarily contain a valid "time
operator".
- The role of space-time is often to define the structure of the experiment. Once the relationships between measuring devices are established, the role of time can often be depreciated. For example, the natural description of a particle trapped in a potential well consists of "stationary" interfering waves. (E.g. Hydrogen atom) Time plays no role.
5.3 Problems with a-prior Spacetime
Quantum Mechanics is incompatable with the General Theory of Relativity (GTR); they are fundamentally different in nature. In GTR, spacetime curvature is determined by energy density (including mass). In Quantum Mechanics, energy arrives in quanta (discrete amounts). Should we expect curvature to be quantized? GTR is a continuous theory! Also Quantum Mechanics is subjective (See Wigner's Friend), but GTR is an objective theory. Yet the Bohr-Einstein discussions show that Quantum Mechanics is consistent with GTR at least to some degree.
The general view in the Physics community is that current concepts of spacetime needs to be reviewed, but it very hard to see how to make progress. String Theory treats Gravity as a force generated by the exchange of virtual particles having universal coupling; mass and inertial frames are artifacts of resulting quantum field. Quantum Loop Gravity on the other hand builds up background spacetime from topological "loops" of spacetime "stuff". Neither of the approaches is really successful. Perhaps another approaches is the correct one? The problem remains a great unsolved mystery.
The fact that the "best" Quantum Clocks produce statistical estimates suggests that time may in fact be a statistical concept like temperature or pressure.
5.4 Desiderata
Great care must be taken with Desiderata (they are a great way to disguise prejudices as high-sounding principles), but this desiderata should be considered as relatively uncontraversial.
- Any fundamental understanding of Quantum Mechanics should not assume a-prior ability to measure space or time.
6. Measurement
6.1 Principles of Real Measurement
Measurement is not a completely mysterious process. There are quite a few statements that can be made, which are summarized by the Principles M1 – M4 below.
M1: Principle of Real Measurement.
M2: Principle of Exact Measurement.
M3: Principle of State.
M4: Principle of Repeatability (a.k.a.
Projection Postulate.
These principles have surprisingly strong consequences, which will be explored in the next few sections. This section will concentrate on a traditional view of the measurement, while later sections will concentrate a more instrumentalist view of measurement.
6.2 (M1) Principle of Real Measurement
M1: A measurement instantaneously and discontinuously changes the probability distribution associated with some R-valued physical quantity.
Classically a measuring device "targets" a physical property. For example, police radar guns "target" the speed of cars and produces a single R-valued number, say accurate to within 0.1 k.p.h. of the "correct" speed of cars.
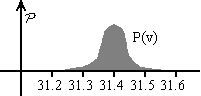
The figure above shows probability distribution for the car's speed after a measurement. The digital readout of the speed gun displays a speed of 31.4 k.p.h - the mean of the probability distribution.
An "exact" measurement of physical quantities is not possible or always desirable. HUP implies that an "exact" measurement of a car’s speed (and hence momentum) would impart an infinite degree of uncertainty with respect to the car's position. An "exact" measurement would result in the random and instantaneous transportation of the car and any occupants to a random location across the universe. It would be a very impressive weapon indeed.
The Principle of Real Measurement does not say "The measurement of a quantity results is a R-valued number". This is a misinterpretation of the formalism of Quantum Mechanics. Instead, a measurement merely reduces the uncertainty associated with some physical quantity. It changes the quantity probability distribution.
6.2.1 Weak and Strong measurements
Strong measurements: A measurement is a strong measurement is the probability density is reduced to zero outside some region [a, b] of R, where [a, b] is not the set of all possible outcomes. The following apparatus shows a strong position measurement.
In the diagram below, a photon source emits a single photon. A photon detector with resolution d is located at the quantum-classical boundary at x =a. If a photon is detected then the resulting probability distribution is zero outside the region [x - d, x + d].
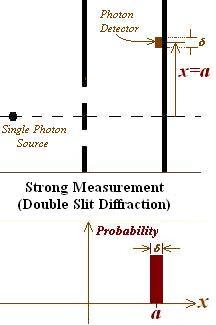
Weak measurements: A measurement that is not a strong measurement.
All known measurements of time are weak. For example, the clock considered in section 6 can only ever produce a "most likely" time. It can never say that the probability that the elapsed time is actually between t0 and t1 is zero.
6.2.2 Why R?
Why are physical quantities R-valued? There are a number of partial rationalisations: Kant pointed out that humans reason with mental models, and those mental models use Natural numbers, and by extension, Real numbers. Bohr considered measuring devices as "essentially" classical; classical physics concentrates on R-valued quantities such as position and momentum. But ultimately that’s just the way the Universe is. Using real numbers however introduces "The Calibration Problem". (See below)
6.3 (M4) Principle of Repeatability – a.k.a. Projection Postulate)
"From physical continuity, if we make a second measurement of the same dynamical variable immediately after the first, the result of the second measurement must be the same as that of the first" - Dirac, 1947.
If two measurement of a physical quantity are made, one immediately after the other, then the probability distribution associated with the quantity immediately after the second measurement must be the same as probability distribution associated with the quantity immediately after the first.
6.3 (M2) Principle of Exact measurement
Measurements at the Quantum-Classical boundary are always 100% accurate. This is sometimes unfairly criticised as tautological: a measuring device measures whatever it measures!
6.4 (M3) Principle of State
Any quantum system is completely described by a state vector Y
and a Hamiltonian H. Knowledge of the previous history of the waveform
is irrelevant to the calculation of the probabilies of any experimental
outcomes. Once the system is known to be in a state Y
then the future state of the system is given by 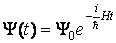 .
The Hamiltonian H characterises the system but does not
contain any information about the current state of the system.
.
The Hamiltonian H characterises the system but does not
contain any information about the current state of the system.
of
Quantum Mechanics
You are strongly advised to consult the pdf version of this document, which is more complete than this webpage. This section is out-of-date and is no longer maintained.
7.1 Mach Devices
According to Bohr, measurement device are essentially classical as they measure classical quantities such as position and momentum. Their physical structure is the result of our knowledge of classical physics and engineering. There are difficulties wtith this approach, including but not limited to:
-
The approach requires a knowledge of classical mechanics before Quantum
Mechanics can be understood, yet Quantum Mechanics is presumed to be more
fundamental than classical physics.
-
It is not easy to apply Bohr's vision of essentially classical measuring
devices to abstract concepts such as QCD color, yet Quantum Mechanics formalism
clearly applies and successful theories have been developed. The concept of
"measurement" is more clearly general than measurement by macroscopic
instruments.
-
It seems unlilkely that an approach which assumes classical spacetime a-prior
will easily shed light on Quantum Gravity.
- Our existing knowledge of classical physics make it difficult to tell which behaviours are fundamental to the measurement process and which are artifacts of our classical knowledge.
In this section measurement will be considered from the perspective of users of "Mach devices". The internal structure of a Mach device is unknown, and users have no a-prior information of what the numbers it produces mean. It is a "black box". Furthermore, the analysis will proceed on the assumption that the user does not have a clock.
The Principle of Real Measurement and Principle of Exact Measurement will be accepted since these carry over to Mach Devices without modification.
7.2 Principle of State
The Principle of State (M3): There is some minimal subhistory Y , called the state of the system, such that P(x | Y) = P(x | full history ) for all x.
The Principle of State says that we can disregard "old" measurements. A history consisting of only the last measurements for each device is just as good as a more complete history (whatever that means) for the purposes of predicting the future.
Why should quantum systems be so simple? Remember we have no clock, so what are the alternatives? Some possibilities:
- Only count the last N (10? 20?) meaurements, but more recent measurements have more "weight" - these sort of schemes play havoc with calculation of natural periods, correlations etc.
- A full description of the systems requires the history of all measurements ever made - which means that we could never make accurate predictions since our knowledge is incomplete for practical reasons.
7.3 Principle of Relativity (Mach's Principle)
Principles M1 - M4 can be found in the literature on Quantum interpretations. The Principle of Relativity is sometimes implicitly discussed, but is not an accepted part of any standard interpretation.
Principle of Relativity (M5): If (1) there is no known relationship between the measurements produced by measuring device and any other measuring device, and (2) there is no prior knowledge of its internal operation, then no meaning can be assigned to the numbers it produces.
This is a generalisation of Mach's Principle. Ernst Mach argued that it would be meaningless to talk about the motion of a single particle in an empty Universe. A person afloat in a boat on a still lake at night in pitch-blackness has no indication of his speed. He could be drifting almost motionless. He could be being pulled along by a swift and silent current. There is no way of knowing. However if the person in the boat can see the shores of the lake, then he can determine his speed relative to the land. All motion is relative. Mach's statement of the Principle of Relativity influenced Einstein but the principle itself dates back at least to Galileo.
A single measuring device is meaningless for the same reason – all measurement is relative. If there is no context, measurements becomes a meaningless stream of numbers.
If we have two measuring devices, say A and B, how do we know what they measure? Do they are measuring the same quantity (in which case we only really have one measuring machine), or do they each measure something completely different?
Providing the measurements are repeatable, a mechanical procedure can be devised to classify the devices as measuring.
- the same quantity, or
- conjugate quantities, or
- separate non-conjugate quantities.
If both devices measure the same quantity, then there is really only one device.
Mach's Principle applies and so any measurements are meaningless.
If both devices measure separate quantities, then again Mach's Principle
applies and any measurements are potentially meaningless.
7.4 The Equivalence Principle
There is no distinction between measurment in the Quantum world and the classical macroscopic world. The distinction arises solely from the way in which measurements are interpreted.
This principle is not to be confused with Einstein's Equivalence Principle. The principle states that there is no Classical world or Quantum world; there are only different interpretations of measurement. (Measurements are regarded as primitive concepts) The easiest way to see this is with a diagram.
The diagram on the left shows "raw" position measurements. The diagram on the right shows the Classical interpretation of the results. The measurements are assumed to be "inaccurate", a particle is assumed to move along the smooth trajectory shown. The diagram in the centre shows the Quantum interpretation of the measurements. There is no presumption about a particle trajectory - only a series of probability distributions showing where the likely location of the next position measurement.
7.5 Derivation of Standard Quantum Mechanics.
It is asserted that the standard Quantum Mechanics can be derived by from the above Priniples above by applying standard probability theory to measurement stream. The reader is referred to the seperate and more comprehensiev overview found at http://www.bowmain.com/QM/London_Interpretation.pdf
7.6 The Calibration Problem
Bohr's view was that measuring devices are "essentially classical" in the sense and the examination of their macroscopic structure determines what they measure. Bohr's approach fails completely when considering abstract properties such as quark color; there is no way to relate quark color to any macroscopic measuring device, yet color is clearly a valid and useful construct. Bohr's approach is useful, but limited. A better approach is needed to handle the ideal, 'perfect' measurements used in theoretical calculations.
The Calibration Problem: Suppose we are in a closed room where
we are presented with a sealed measuring (Mach) device of unknown origin and
construction which produces a stream of (![]() valued) measurements. How do we know what the device is measuring?
valued) measurements. How do we know what the device is measuring?
Proposition: The commutator relationship between operators define "what we are measuring". The classic case is Angular Momentum.
The proposition has several advantages:
- The commutator relations can be extracted experimentally (with some limitations) from a measurement stream (even though it may be very computationally expensive)
- Commutators do not require Classical Physics to pre-define the concepts required for use by Quantum Mechanics.
- Commutators naturally define a local "scale". If X ® f(X), then the commutator relations change ( [X, Y] ® g(X1 .. Xn))
The major problem with the proposition is that we are currently not in a position to formulate physics purely in these terms; it remains unfinshed work.
8. Time revisited
The nature of Time presents us with real difficulties. The mathematical structure of Quantum Mechanics implies that there is no time operator; it cannot be measured in the same way as other quantites such as position, spin or momentum. It is not possible to build an accurate quantum clock, yet time appears in Quantum Mechanics equations as a mysterious parameter - arising from the fact that all real systems are embedded in a pre-existing 4-dimensional space-time.
It is possible to build a quantum clock, just not a particularly accurate one. The construction goes like this: Assemble a large number of indentical particles. Each particle can exist in one of two states: an excited state and a ground state. All the particles are put in an excited state and kept there. The clock begins to run when the particles are allowed to decay naturally to the ground state. Time is measured by counting the number of particles in each state (see formula below); the more particles in the ground state the greater the amount of time passed since the clock began to run.
Rocks and fossils are dated using just this type of "atomic clock".
It may be that time can only be defined by the clock construction above. I.e. time is a statistical concept like pressure, and like pressure, it has no meaning at very small scale. If this is so, all theories that assume the existance of a smooth background space-time, such as GTR and String Theory, are doomed to fail at the very small scale (plank scale).
9. String Theory - RFC
String Theory is an "obvious" mathematical generalization of Quantum Mechanics. Strings propogate in the same manner that "particles" do in Feynman's world. If the popular press is to be believed, String theory is close to explaining all quantum phenomena. It is the "Theory of Everything".
The problem the author has with String Theory is that it is hard to understand the physics of String Theory, as opposed to its mathematical content. What happens when a string is "measured"? Does a "position" measurement return only the "average" position of the string? The location of an end-point? If so, which end-point? Does it return the position of some point along the string? (The string is a 2D object extended in space - its position cannot be described by a finite set of numbers and therefore cannot be described by a finite set of measurements) Does HUP apply to the whole string? Or does it only apply to the "section" of the string being measured? If the "position" of a string is measured with abitrarily high accuracy, what happens to the momentum of the string? Does the "momentum" become undefined (as opposed to simply unknown)? How does Bell's inequality apply to string theory? Does String theory modify HUP? No doubt the answer to these questions could elude the author simply because of his lack of knowledge of String theory. String theory may be a straight-forward extension of the mathematics of standard Quantum Mechanics, but its interpretation is less than obvious. The other possibiilty if that String Theory is just wrong.
David Deutsch, Professor of Physics at the University of Oxford's Centre for Quantum Computing, says "In the last few decades, many theoretical physicists have assumed that further progress can only come from looking at new mathematical models and then wondering if the models are true representations of nature. An example is String Theory. I think it's unlikely that a research program of that kind can work. Even if you found the right mathematical object, you probably wouldn't even recognise it because you wouldn't know how it corresponds with the real world. For example, if someone had invented quantum theory purely as a mathematical model, how would they ever guess that its multi-valued variables correspond with the quantities that we measure with single values? After all it assigns multiple values to observable quantities simultaneously. I would warn against expecting the answer to come from a new mathematical model. It should be the other way around: first find what you think might be the solution to a problem, then express it as a mathematical model, then test it".[7]
The author seeks contributions from readers who feel they can present interpretations of String Theory.
10. So what have I learnt about Quantum Mechanics?
There is nothing on this page that can't be found somewhere in a textbook, however it seems to me that the treatment of the interpretation of Quantum Mechanics by most textbooks is incomplete. Many textbooks, for example, only present enough to contrast Quantum Mechanics with classical physics or use a semi-historical approach.
There are many reasons why a detailed discussion of interpretation is avoided, but mostly I think the reason is this: Interpretations are contraversial. It is impossible to prove an interpretation in the same manner as it is possible to prove the correctness of the predictions of Quantum Mechanics itself. No doubt there is a feeling that a discussion on interpretations would be frustrating and ultimately pointless, as well as detracting from huge areas of pratical interest such as Quanutm Chemistry, Solid State Physics etc. Anyway students "pick up" a working interpretation of Quantum Mechanics based on the language used to solve problems; only "advanced" or "interested" students would feel any need to explore interpretations. Perhaps it would be best to leave interpretations to the philosophers and new-age hippies. Hmmm....
One wonders how many physicists who purport to support particular interpretations actually understand them.
-
Subtle is the Lord. Quantum Mechanics is not "rife with uncertainty and riddled
with paradoxes" [8] , but the analysis of many situations
require great thoughtfulness and care with language.
-
In the author's opinion, only the Copenhagen Interpretation is
viable. (See above for the justification for this
statement) Many-worlds and other interpretations make for rattling good Star
Trek stories, but that's not the way the world is.
-
The Copenhagen Interpretation is a strict positivist interpretation. Quantum
Mechanics is just a probability calculus which can be applied to a specific
combination of measuring devices and quantum system. The waveform has no
reality. There is no waveform collapse.
-
Consistent Histories concentrates on applying standard logic and probability
theory to a specific choice of sample space ("framework"). Consistent Histories
provides more rigorous versions of some of earlier statements of Copenhagen
such as Bohr's Complementary Prinicple. Unfortunately other aspects of
Consistent Histories, such as a real waveform, render this interpretation
non-viable.
-
Hidden variable theories cannot be ruled out, but no-one has come close to
producing a real alternate to standard Quantum Mechanics.
-
The correspondence between the Copenhagen Interpretation and the Bayesian
interpretations of classical probability theory is so complete that it is
possible to view the Copenhagen Interpretation simply as
(i) Heisenberg's Uncertainty Principle, plus (ii) Bayesian interpretation of probability (unreal waveform), plus (iii) Positivism (no deeper meaning than that obtained through measurement)
Many of the statements of non-reality and subjective probabilities that some physicists find so disturbing find equivalent statements in modern "classic" probability theory. However the history of classical probability does not bode well for the resolution of the battle between competing interpretations. Classic Probability theory is hundreds of years old, but there is still an active debate about which interpretation is correct.
-
Bohr got it pretty much right
References
1. "The Meaning of Quantum Theory" by Jim Baggot
2. "Feynman Lectures in Physics, Vol III" by Richard Feynman.
3. "Surely you must be joking" by Richard Feynman.
4. Einstein A., Podolsky B. and Rosen N (1935). Physical Review. 47,777
5. "Probability Theory, The Logic of Science" by E.T.Jaynes
6. "The Critique of Pure Reason" by Immanuel Kant. Translated by J. M. D. Meiklejohn, eBooks@Adelaide. 2004
7. "At play in the multiverse", New Scientist, 9 December 2006.
8. New Scientist - Instant Expert:Quantum World.
9. Larry Sanger - co-founder of Wikipedia, quoted in Information World Review (and many other sources), 13 April 2007.
Thanks
1. Tx to Robert Watson, Peter Kirby
Feedback
If you find an inaccuracy in any of the above please e-mail me at sokane@bowmain.com.
Copyright (c) Shaun O'Kane, 1997, 2002, 2005, 2006, 2007, 2010. You are free to redistribute this work provided you give due credit to it's author.