QUANTUM MECHANICS - WHY THE KERFUFFLE?
BEFORE QUANTUM MECHANICS
Why does Quantum Mechanics challenge our view of the world so much more than even Relativity?
To appreciate Quantum Mechanics it helps to know what the world was like before it came into being.
That world was Newtonian.
The world was made up of matter, forces, space and time. If we wanted to know to know how a piece of matter would move, we would need to calculate the forces F acting on the matter as well as know its mass m (directly related to its weight). The acceleration of the matter would then be calculated by plugging the numbers into the simple formula
The forces on the object were calculated by rules extracted from experience. For example, the force generated by a spring was given by Hookes Law
where k is a characteristic of the spring that can be directly measured, and δx is the amount the spring is extended or compressed.
Newtonian Physics was astoundingly successful. The matter in fluids could theoretically be cut up into “infinitesimal small” cubes and relatively simple Newtonian laws applied to them. The resulting equations, such as Navier-Stokes, showed that even exquisitely complex phenomena such as turbulence had a simple, common explanation.
Isaac Newton (1642 - 1727) himself had introduced the Universal Law of Gravity. Every piece of matter in the Universe attracted ever other piece in the Universe. The attraction was extremely small for everyday things, certainly undetectable in Newton's day, but when applied to celestial objects such as comets and planets, F=ma had managed to predict and explain the motion with unheard of precision. Neptune had been discovered as result of a search for an unseen planet causing minute discrepancies in the predicted orbit of Uranus.
Laws for the conservation of energy, momentum and angular momentum were developed. The understanding of the conservation of energy proving very useful in the development of thermodynamics.
Electrical and Magnetic forces had entered into the Newtonian fold in the latter part of the 19th Century. Clerk Maxwell (1831 - 1879) had written down equations that described electrical and magnetic fields, and those equations had predicted that waves of electrical and magnetic change could propagate through space at a speed that matched the measured speed of light. It did not take much for it to be accepted that light was indeed an Electro-Magnetic phenomena.
Everything looked rosy in the Newtonian garden. Newtonian physics had proved flawless in it's predictions for 200 years. There was no reason to believe that things wouldn't stay that way.
A FLY IN THE OINTMENT
A few, rare individuals had guessed that other options existed and seriously considered them.
Georg Riemann (1826 - 1866) wondered if the Geometry of the world was not Euclidean. He climbed the Alps with a theodolite to check that the angles of a triangle did indeed add to 180o.
The advance perihelion of the planet Mercury (the point were it is closest to the sun) was unexplained, but confidence was high that problem would be resolved. It wasn't until 1916 when Einstein introduced General Relativity.
Ernst Mach (1838 - 1916) felt uncomfortable with the concept of an inertial frame (basically a non-accelerating observer). He proposed that an inertial frame was one which was at rest or constant velocity with respect to the average mass of the universe, although he had no Mathematics to solidify his idea.
However while Newtonian physics seemed infallible, such criticisms remained moot.
In 1905 that changed. Albert Einstein (1879 - 1955) noted that Maxwell's equations predicted that the speed of light was
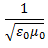
where ε0 and μ0 are constants.
No other physicist had thought through the implications. Either the speed of light was constant as predicted by Maxwell, or Maxwell's equations were only correct in one frame of reference and had to be modified in all others. After much thought, Einstein came to the conclusion that there was no special frame of reference and the speed of light was indeed constant.
The problem with this is that in the Newtonian world, speed is additive. If I am travelling at 30 km/hr and you pass me at 40 km/hr, then I know that your speed is 70 km/hr.
If a light beam leaves my torch at 300,000 km/hr, and you are travelling at 40 km/hr relative to me, you would expect to see the light beam leave my torch at 299,960 km/hr, not 300,000 km/hr.
The answer that Einstein came up with is that time passes at different rates for different observers. Light is not seen to travel at 299,960 km/hr because time passes more slowly for a moving observer.
Einstein also realised that observers do not agree about which events happen simultaneously. And matter was seen to be stored energy, related by the famous equation
This book however is not about Relativity. Relativity is well understood. It's interest to us is that it was the first real challenge to the Newtonian hegemony.
ATOMS
The theory of atoms predates even Newton and goes back to the ancient Greeks. They asked the question: if you keep cutting a substance in half, what would happen? If you continually cut a piece of cheese in half, would you always get cheese?
Leucippus and Democritus (460 BC - 371 BC) decided the answer was No. They proposed that matter is made up of small, eternal, indivisible particles called atoms; atoms of the same type being identical in all respects. They originally assumed only 4 types of atoms: air, water, fire, earth.
John Dalton (1766-1844) and others proposed that atoms could be used to explain the weights and proportions of compounds produced and consumed in chemical reactions. By 1860, 60 elements were known; an element being a substance composed of only a single type of atom. In 1869, Mendeleyev (1834 - 1907) produced the first chemical periodic table.
The concept of atoms was used to explain the properties of gases. Ludwig Boltzmann (1844 - 1906) developed a statistical description of the motion of atoms/molecules in gases.
The existence of atoms was still controversial by the beginning of the 20th Century. Bitter debates, frustration and rejection ultimately lead to Boltzmann's suicide (1906). In 1905, Einstein published a paper on Brownian motion. Small grains of pollen "judder" about under the microscope as the result of atoms crashing into them at high speed. Within a few years of publication, the existence of atoms became universally accepted within the scientific community.
THE REVOLUTION BEGINS
1876 - Eugen Goldstein produces "Cathode rays" (electron beams).
1896 - J.J. Thomson shows Cathode rays are beams of negatively charged particles with a mass less than a thousandth of that of the lightest atom.
1896 - The scientific community settle on the name "electron" for Thomson's particle.
1900 - Max Plank produces a solution to the "Ultra-violet Catastrophe" by assuming that energy is quantised. The result was generally viewed as a curiousity until 1905 and Einstein's paper on the Photo-electric effect.
1905 - Einstein published "On the Electrodynamics of Moving Bodies", the contents of which has come to be known as Special Relativity.
1905 - Einstein published a paper which explain the Photo-electric effect by assuming light is a particle.
1911 - Rutherford bombards gold foil with alpha radiation. Most alpha particles go straight through the foil showing that the atoms that make up the foil are mostly empty space. A few hit a heavy "nucleus" and richocet back through sharp angles. Rutherford proposed the moderm model of an atom - the nucleus (centre) of the atom consists of a heavy positive charge surrounded by lightweight negatively charged electrons.
PHOTO-ELECTRIC EFFECT
It was Einstein's explanation of the photo-electric effect that ultimately was the most radical of his amazing papers published in 1905.
What is the photo-electric effect?
If light shines on some types of metal in a vaccuum, the light will absorbed and an electron emitted.
The phenomena has been used to create "electric eyes" that detect machines or people who break a light beam, triggering an alarm or starting or stopping some mechanical process. The technology has largely been superseded
The interesting bit is the way the metal responds to the light. If light is a wave, the wave should should start to slowly impart energy to the electrons in the metal. At first there would be no reaction to the light. After a period of time, the electrons build up enough energy to break free of the metal and a large number of electrons are emitted across the surface of the metal. The emitted electrons should not be very energetic (not emitted at speed) since they only just had enough energy to break free of the atoms.
Lower frequency light has a lower energy content for the same intensity so it takes lower frequency light longer to emit electrons.
That's not what happens.
Instead the metal react instantly, emitting electrons as soon as the light is turned on. Furthermore the electrons are energetic. There is also a cut-off frequency below which electrons will not be emitted. The energy of the emitted electrons is directly related to the frequency of the light - the higher the frequency of the light, the higher the energy of the emitted light.
Einstein's solution was simple. Light consists of photons (particles!). The higher the frequency of the light, the higher the energy of the photon. If the photon strikes the metal atom and is absorbed, the energy of the photon is immediately passed to the electron. Assuming the photon has enough energy, the electron breaks free of the atom and the energy of the emitted atom is equal to that of the photon minus the binding energy of the atom. If the photon does not have enough energy to cause the electron to break free, it is not absorbed.
IS LIGHT A WAVE OR PARTICLE?
Light sometimes behaves like a wave and sometimes behaves like a particle. But it can be neither.
This simple statement is sometimes called "Wave-Particle Duality".
It has caused more denial and contorted mental gymnastics than probably any other in the physical sciences.
Wave-Particle Duality is at the heart of Quantum Mechanics.
There are still theorists who devote their efforts to prove this is not the case, it just looks that way. There efforts are almost surely futile. The author's advice is don't become one of them.
THE REVOLUTION CONTINUES
1924 - Louis De Broglie suggestsed in his Ph.D. thesis that all matter may have a dual character, sometimes acting like a wave and sometimes like a particle. De Broglie even suggested the wavelength that a matter wave would have.
It has been reported that the idea was a little too radical for De Broglie's supervisors and De Broglie was initially denied his Ph.D. De Broglie sent his thesis to Albert Einstein who approved, and De Broglie was granted his Ph.D.
1927 - P.G. Thomson, son of J.J. Thomson who showed electrons are particles, demonstrated electon diffraction - a wave phenomena.
It was now apparent that the paradox of wave-particle duality is not just a problem for light. It is problem for all of physics.
Perhaps not surprisingly two separate Quantum theories appeared overnight: wave mechanics that concentrates on the wave characteristics of light and matter, and matrix mechanics which is much more abstract and concentrated on measurements.
It didn't take long for P.A.M Dirac to demonstrate that they were different mathematical formulations of the same more abstract theory ... Quantum Mechanics.
IS MATTER A WAVE OR PARTICLE?
What do atoms look like?
Version 1 - The classic atom
The picture of the atom taught at school resembles that of the solar system. A heavy nucleus sits at the centre of the atom playing the part of the Sun. Smaller lighter electrons play the part of the planets orbiting the nucleus. The force of gravity is replaced by electrical attraction – each electron carries a single negative charge and is attracted towards the positively charged nucleus.
The "classic" picture of an atom slowly emerged from a series of experiments.
- Milikan's experiment showed that charge was quantised - charge is lost or gained as additional electrons are lost or gained.
- Thomson demonstrated the existence of negatively charged particles (electrons) using Cathode Ray Tubes.
- Rutherford demonstrated that most of the mass of an atom resided in a small positively charged core by firing alpha particles at thin gold foil. Most of the particles passed through the gold foil as if it consisted of empty space (because it mostly is). A few struck the nucleus, recoiling back at sharp angles and allowing for the calculation of the size of the nucleus.
- Chadwick discovers the neutron (required to explain atomic weights)
Is the classical picture correct?
The model is fine for teaching purposes in junior high school. Classical Electromagnetic theory however suggests that the electron should rapidly spiral down and crash onto the nucleus, radiating energy as it goes. That's not what happens - atoms are stable. The model is wrong.
Version 2 - The electron cloud
The second picture of the atom is based on a niave interpretation of the equations of QM discovered by Schrodinger. Atoms are portrayed as a nuclei surrounded by electron clouds. (Electrons swarm around the nuclei like flies around a cowpat ).

Is the electron cloud picture correct?
The electron cloud model is based on the equation of QM. It is adequate for computational applications, including most of Quantum Chemistry and Quantum Mechanics. In particular it is (often) possible to to calculate or estimate such things as atomic energy levels, the spectrum of emitted and absorbed radiation, strength of chemical bonds and the properties of materials.
Problems only arise if one looks closely.
Quantum Waves
Light is a wave. Or is it?
By the beginning of the 20th century, it was generally regarded that
experimental evidence such as diffraction showed light is a wave.
Maxwell Equations (1875) predict waves of Electromagnetic radiation. It is
suggested light is a form of electromagnetic radiation. The speed of light
predicted from Maxwells Equations matches the measured speed of light.
But...
Max Plank use his "quantum" hypothesis to explain the spectrum of black body
radiation.(1901).
Einstein (1905) produced his light quanta (particle) hypothesis to explain the
photo-electric effect.
Electrons are particles. Or are they?
J.J. Thompson demonstates particle nature of electrons using cathode ray tubes (1897).
But...
De Broglie (1924) suggests that matter might also behave like a wave in his
doctoral thesis, which would have been rejected had it not been for the
intervention of Einstein.
Davisson, Germer, Thompson (son of J.J.Thompson) demonstrate electron
diffraction in a crystal (1927) - i.e. experimental proof that electrons behave
like waves.
Schizophrenia
Experimental evidence now indicates that all sub-atomic particles can be made to demonstrate both particle and wave like properties. How can the two behaviours be reconciled?
In fact, the "best" description of the motion of a particle like an electron is that of a wave moving through space. It can be diffracted. Whenever energy is transferred form the wave, the energy is transferred as a quanta. QM only describes the motion of the wave. The transfer of energy from the wave cannot be predicted precisely, the best we can do is calculate probabilities of an interaction.

The diagram at left shows the result of a double slit diffraction experiment. QM predicts a waveform with alternating bands of high and low intensity. Frames (a)-(d) show snapshots over time as individual particle "arrive" (transfer energy) to the screen. Initially it is difficult to see any pattern (a)-(b). As time goes on, the waveform reveals itself (d).
It is tempting to think of electrons "hiding" inside the wave, only emerging when interacting with some other part of the world. But, as we shall see, that would probably be a step too far.
Quantum waveforms are complex valued. and interfere destructively. Probability waves are always "positive" and cannot interact distructively. If Y(x,t) is the waveform describing the state of a particle, then the position probability distribution P(x,t) is given by the formula
Why? A very good question. If you can come up with a really good reason for this, you will have solved one of the truly great mysteries of the Universe.
Notation
Dirac bra-ket notation is sometimes used to descrive quantum waveforms. For example, the waveform describing a electron might be denoted |e- >, the waveform describing a sperm whale might be denoted |whale>.

Heisenberg's Uncertainty Principle
Heisenberg's Uncertainty Principle (HUP) lies at the heart of Quantum Mechanics. Without HUP, QM would be inconsistent.
To see that this is so, ask the question: Why are we forced only to deal with probabilities? In the case of an electron moving through space, why can we not build a measuring device and just measure the position of the electron? There are obvious engineering problems, but for the moment let us suppose that it can be done. QM certainly does not preclude the construction of such a machine.
To completely avoid probabilities, it would be necessary to also measure the electron's momentum. Once both the position and momentum are known, then it possible in theory (at least in classical theory) to calculate the position of the particle precisely into the future.
HUP kicks in: It is not possible to obtain exact measurements of both position and momentum. It is therefore not possible to bypass the probabilistic description of nature.
More precisely, HUP looks like
where sx is the standard deviation of the probability distribution of a particle's position (x), sx is the standard deviation of the probability distribution of the particle's momentum (p), h is Plank's constant = 6.625 x 10-34 J-s. HUP guarantees that the more "precise" the information available about a particle's position is, the greater the uncertainty in the particle's momentum. Even if the a particle's momentum had been previously be determined with a high degree of accuracy, any measurement of the position would destroy the validity of the first measurement of momentum. Similarly the more precise the information about a particle's momentum is, the greater the degree of uncertainty in the particle's position. It is simply not possible to make accurate measurements of both position and momentum at the same time.

HUP applies to sub-atomic particles, people, cars, galaxies, sperm whales and bowls of petunias, but Planks constant is very small. At normal energy (amd momentum) levels, the uncertainty in position of an electron is (not surprisingly) roughly the size of an atom.
Absorption and Emission of Radiation
Quantum Mechanics predicts that the energy levels of an atom are quantised; the energy levels are characterised by quantum numbers.
Chemists use the misleading term "orbitals" to describe the waveforms associated with each energy level. They also, for historical reasons, refer to the orbitals by letter (s,p,d,f) rather than quantum number. The figure below shows the shape of the various "orbitals". Note however that the orbitals do not have sharp boundary; rather the probability of finding an electron gradually drops off with dstance from the nucleus.
Protons and neutrons in an atomic nuclei behave in similar way to electrons in an atom; models using "orbitals" can be used to predict the stability of atomic nuclei. The pattern of stability is not the same as that of the periodic table since the energy levels associated with the nuclear orbitals do not match their atomic equivalents, and therefore each nuclear "shell" contains a different number of orbitals than the equivalent atomic shell.
Atoms randomly make transitions from high energy states to low energy states. If an atom starts in a state with energy E0 and ends up in a state with energy E1, then the difference in energy E0 - E1 will be carried away as a photon. The result is that radiation (radio waves, micro-waves, infra-red, light, ultra-violet, x-rays) emitted by an atom have very precise frequencies, giving rise to characteristic spectra.
The process works in reverse. Atoms may randomly "absorb" passing photons, but only if the energy of the photon matches the difference between its existing energy state and a higher energy state. If the photon is absorbed, the atom goes into the higher energy state.
Tunnelling
In general, the probability distribution of finding a particles at any point in space is not zero, rather it tapers off slowly approaching zero as the distance from the distribution mean increases.That allows particles to "tunnel" through any barrier, even the event horizon of a black hole. However the probability of a macroscopic object like a car tunneling through a barrier like a brick wall is almost zero.
HUP applies to measurements of time and energy. Mass is energy. It follows that a vacuum can create particles out of nothing - provided that they do not live longer than that the time interval predicted by HUP.
Double slit Diffraction
Double slit diffraction is the example of quantum behaviour par excellence. Feynman claimed that if it was possible to understand diffraction, then it was possible to understand all of Quantum Mechanics. A double slit diffraction apparatus consists of (1) a particle source - typically a light or electron source, (2) a screen with 2 parallel slits through which particles can pass, and (3) a screen where the particles that have passed through the double slits arrive. The characteristic double slit pattern is shown in the diagram below and can be understood as a result of "waves" interfering with each other.

Which slit did the electron go through?
It is tempting to consider the possibility that the interference pattern results from particles going through one slit interfering with the motion of particles going through the other slit, however it is possible to set the apparatus up so that statistically only one particle passes through the double slit apparatus at a time; the standard double slit interference pattern is still seen. That means that the photon or electron "interferes" with itself!
Richard Feynman came up with an intuitive method of calculating the probabilities of any event (E.g. the particle in a double slit diffraction arriving at the point A in the diagram below): (1) Draw diagrams showing every possible interaction, (2) calculate the amplitude of the event given the interactions in the diagram, and (3) add the amplitudes for each diagram together. The existance of virtual particles significantly increases the complexity of calculations.


Copyright (c) Shaun O'Kane 2003.